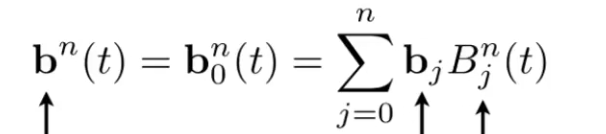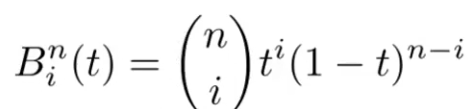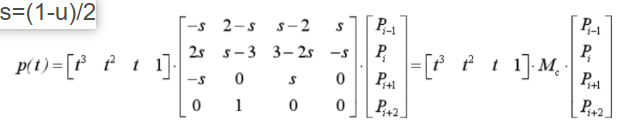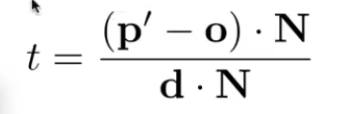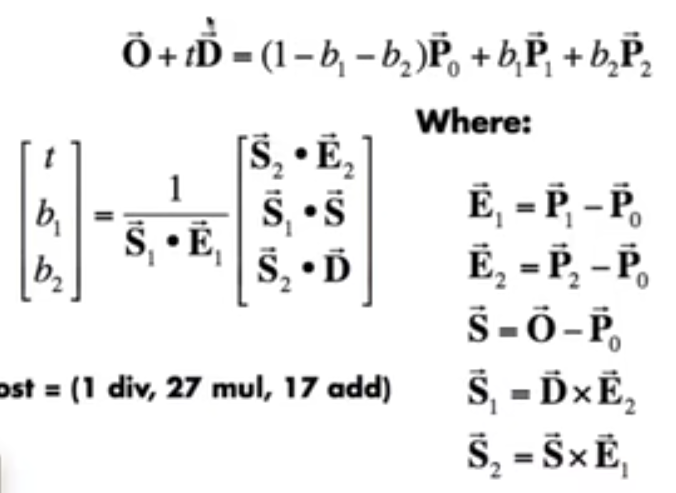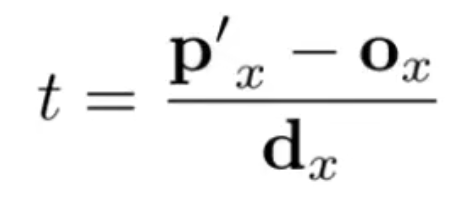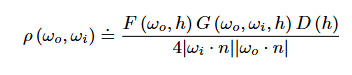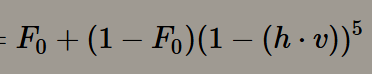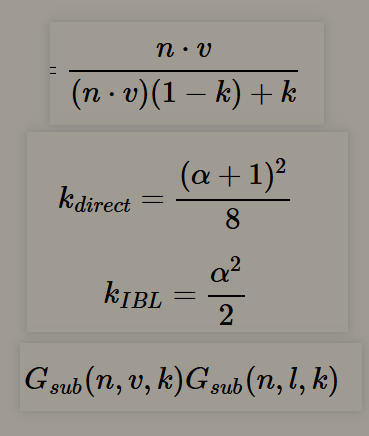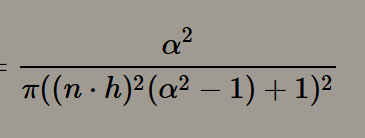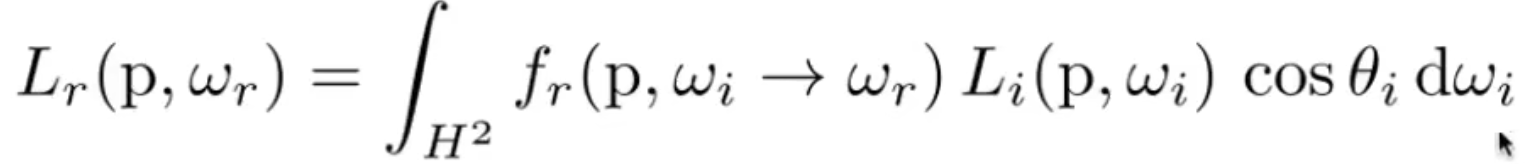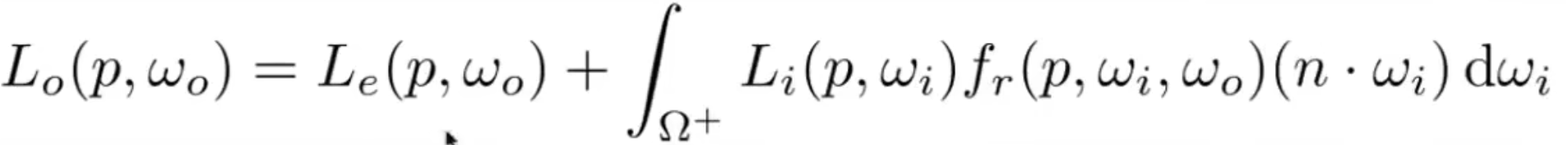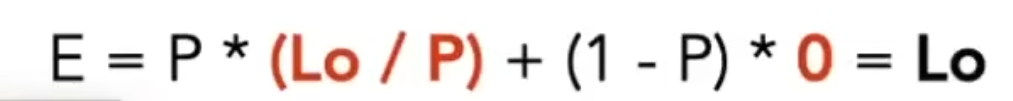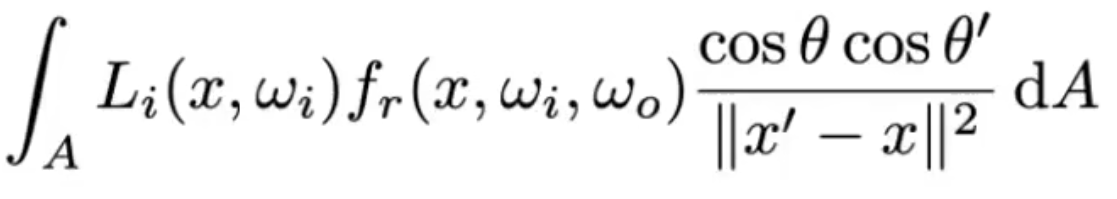101复习(5`几何、光线追踪)

发表于 2025/09/05

作者 senlongan

45 分钟阅读

几何

隐式：
- 数学表达式
- bool运算：并集，差值，交集
- 距离函数SDF：两个物体求得距离函数后混合，可以得到有趣的几何体
- 分型
- 缺点：很难知道哪些点满足表达式
- 优点：容易判断一个点是否满足表达式，将点带入表达式，如果结果为负在物体内，0在物体表面，为正在物体外
显示
- 图元（点云，线（直线/曲线），三角形）
- 参数映射方法，由2维空间转换到3维空间的函数
  - 优点：很容易知道包含哪些点
  - 缺点：很难判断一个点是否在表面上

曲线

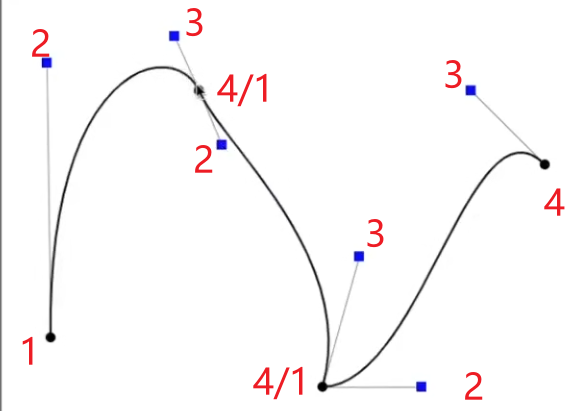
贝塞尔曲线

曲线特点：
- 第0层有m个控制点，则称为m - 1次贝塞尔曲线，比如有4个控制点，为3次贝塞尔曲线
- 曲线一定经过第0层的起点、终点控制点，但不一定经过第0层的中间控制点
- 曲线一定在第0层所有控制点形成的凸包内（包裹所有图形的最小范围）

德卡斯特里奥算法——循环：

思想：已一定步长取t（0——1）的值，每次根据t逐层插值生成新的点，当到达最后一层，将此生成点作为贝塞尔曲线点之一

pair<double, double> linearInterpolation(
  const pair<double, double>& p1, const pair<double, double>& p2, double t) 
{
    return {(1 - t) * p1.first + t * p2.first, (1 - t) * p1.second + t * p2.second};
}
vector<pair<double, double>> calculateBezierPoints(
const vector<pair<double, double>>& controlPoints, double stepSize) 
{
    vector<pair<double, double>> points;
    for (double t = 0; t <= 1; t += stepSize) {
        vector<pair<double, double>> lastPoints = controlPoints;
        while (lastPoints.size() > 1) {
            vector<pair<double, double>> newPoints;
            for (size_t i = 0; i < lastPoints.size() - 1; ++i) {
                pair<double, double> newPoint = linearInterpolation(lastPoints[i], lastPoints[i + 1], t);
                newPoints.push_back(newPoint);
            }
            lastPoints = newPoints;
        }
        points.push_back(lastPoints[0]);
    }
    return points;
}

展开

具体实现：
- 输入第0层所有控制点controlPoints，和Δt
- points用于存储所有贝塞尔曲线点
- lastPoints用于保存上一层的生成点，每次循环会首先初始为第0层的控制点controlPoints
- newPoints用于存储当前层新生成点
- while控制点==1时，将唯一的生成点，加入到points中

伯恩斯坦多项式——算法：
- n == m - 1，即n次贝塞尔曲线
- b0^n：最后一层，最后生成的控制点（即贝塞尔曲线点）
- j：第0层的点索引，为0——n
- bj：第0层的点坐标pair<double, double>
- Bj^n：伯恩斯坦多项式/基函数
- （n i）二项分布：详见概率统计学章节
- 根据这个公式，可以快速求得，对于n次贝塞尔曲线，在t时，对应的贝塞尔曲线点坐标
分段考虑
- 将起始和终点连接，有的中间控制点在线段的一边，有的在线段的另一边，这样是可以生成曲线，但并不直观
- 我们分段考虑，每4个点生成一条曲线
- 如何保证各个分段平滑过渡
  - 上一段终点==下一段起点
  - 上一段的最后两点方向，这一段前两点方向，方向一致，长度相同

三次参数样条曲线
- 当我们当已知某些点而不知道具体方程时候，有两种做法去采集数据：拟合或者插值，拟合不要求经过已知点，插值保证已知点都会经过
- 贝塞尔曲线是一种拟合思想，对于第0层的哪些中间点，不会保证经过它们
- 三次参数样条曲线是插值的思想，可以保证经过所有已知点（控制点）
- 思想：
  - 假设有n+1个控制点，用xi(xi,yi)表示
  - 每两个点组成一个区间[xi,xi+1],总共有n个区间
  - 每个区间都是一个三次方程，称为三次样条函数Si(x),组成总的三次参数样条曲线S(x)
- 三次样条函数满足以下条件：
  - 插值过点：S(xi) = yi
  - 曲线光滑：S(x)，S(x)，S`(x),连续
  - 形式：yi = ai + bix + cix^2 + dix^3
- 构建方程：
  - 每个区间有4个未知数abcd，总共n个区间，也就是4n个未知数，需要4n个方程求解
  - 首先对n-1个内部点，有方程：Si(xi+1) = yi+1, Si+1(xi+1) = yi+1(Si(xi+1)表示[xi, xi+1]区间上的索引为xi+1的控制点，Si+1(xi+1)表示[xi+1, xi+2]区间上的索引为xi+1的控制点),这样建立了2（n-1）== 2n - 2个方程
  - 对于两个端点分别满足：S0(x0) = y0, Sn-1(xn) = yn，现在总共2n个方程
  - 对n-1个内部点，有方程：Si`(xi+1) = Si+1`(xi+1), Si``(xi+1) = Si+1``(xi+1)(因为它们是同一个点，导数应该相等),这样又新增了2n - 2个点，现在总共有4n-2个方程了
  - 剩余的两个方程通过边界条件得到：
    - 自然边界：S” (x0) = 0 = S” (xn),两个端点的二阶导数都==0
    - 固定边界：S0’ (x0) = A, Sn-1` (xn) = B，两个端点的一阶导数分别==A和B
    - 非节点边界：S0``` (x0) = S1``` (x1), Sn-2```(xn-1) = Sn-1``` (xn)，第一个点的三阶导数等于第二个点的三阶导数，最后第一个点的三阶导数等于倒数第二个点的三阶导数
- 解未知数
  - 推导过程就不细说了，大致推导步骤就是根据上面的方程式，带入某点化简消元
  - 此线性方程组，属于三对角矩阵，可以使用Thomas算法解，详见线性代数章节
Cardinal曲线
- Cardinal曲线也是插值的思想，可以保证经过所有已知点
- 张力参数u：控制曲线形状，取值[-1,1]
- t和贝塞尔曲线一样
- 依赖相邻的4个点：Pi-1, Pi, Pi+1,Pi+2，去在pi——pi+1区间生成点
对比：
- 贝塞尔曲线不过点
- 三次参数样条曲线平滑度最好
- 三次参数样条曲线性能消耗较高
- 贝塞尔曲线，可以支持局部修改不影响整体（分段），也可以普通计算影响整体
- 三次参数样条修改一个点会影响整体（mi决定ci的值，ci的值决定第i段曲线形状，mi的值依赖于mi+1，mi+2，而mi+1的值又依赖mi+2，mi+3……）
- Cardinal曲线修改一个点只会影响相邻的部分（因为只依赖相邻点），不会影响整体
- 因此简单易用不需要过点选择贝塞尔曲线
- 想要更平滑的曲线选择三次参数样条曲线
- 想要局部控制选择Cardinal曲线

曲面
- 贝塞尔曲面
  - 比如给4*4 16个点，先从u方向，生成4条贝塞尔曲线，根据时间t，沿着v方向，查找4个曲线上的控制点，生成数条贝塞尔曲线
网格细分
- 细分：将由三角形面表示的网格，增加三角形数量
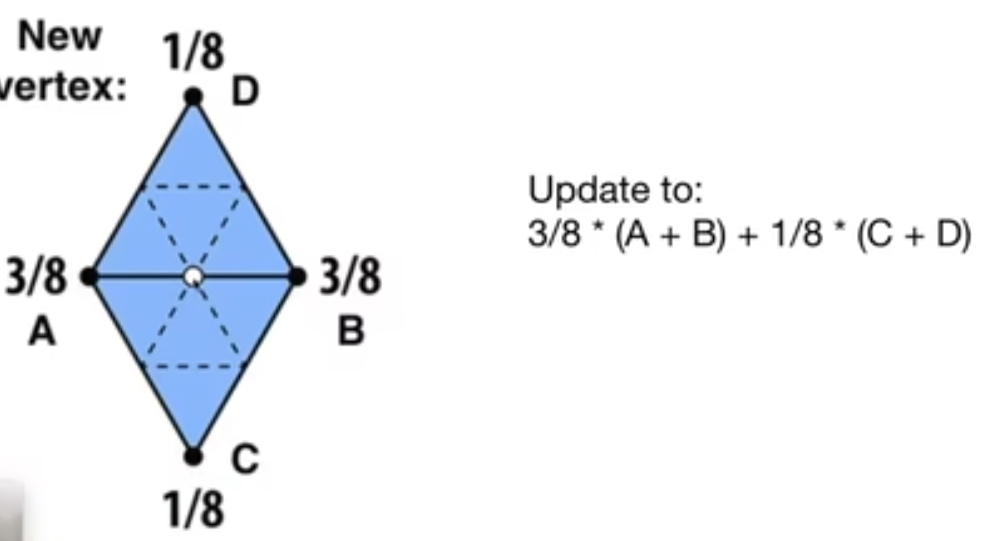
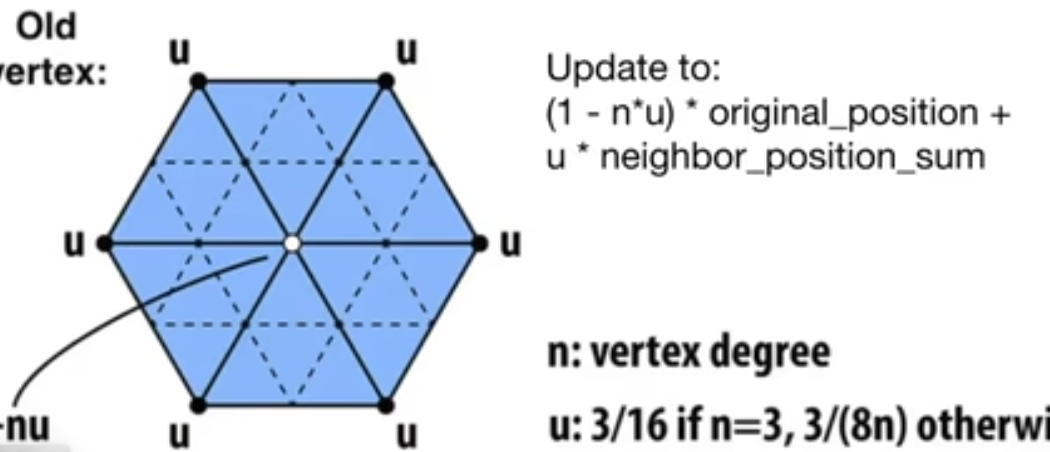
  - loop细分
    - 引入点：将一个三角形变为3个三角形，连接各个边的中点
    - 移动点：
      - 区分新增点和旧点，我们将根据不同规则移动位置，使得网格体更加平滑
      - 新点：找到菱形区域，ab，cd，根据公式线性差值
      - 旧点：找到6边形区域，n是和中心点相连的边的数量，u为周围旧点数量
    - 局限：仅限于三角形网格
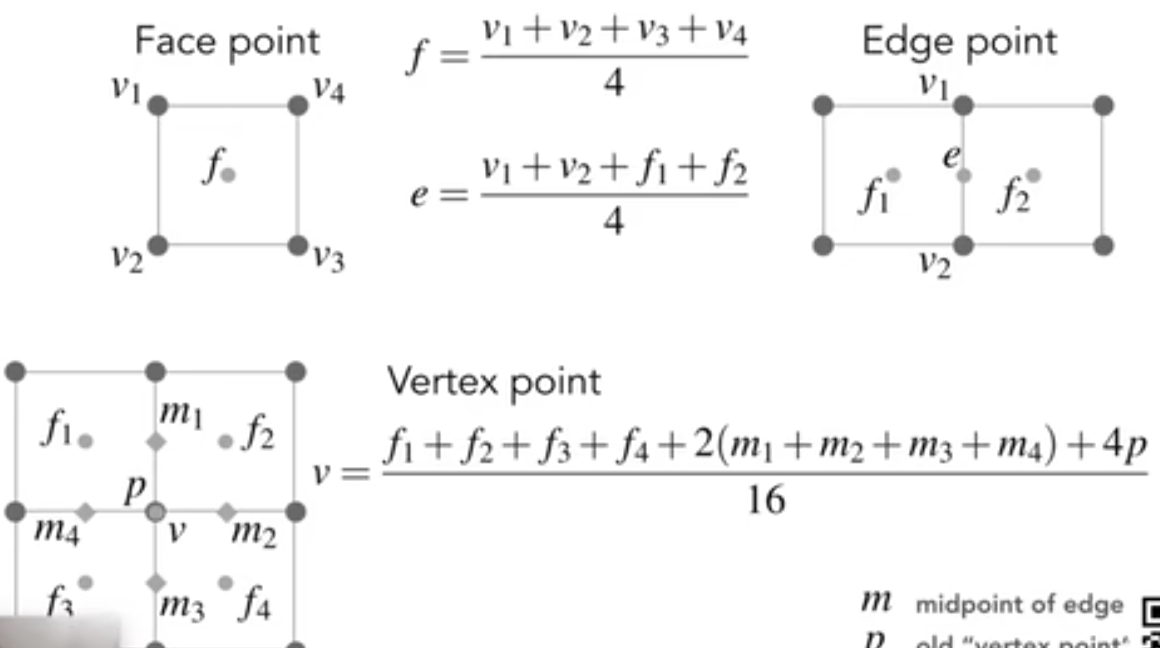
  - catmull clark细分
    - 对于非三角形网格比如四边形网格
    - 四边形，非四边形，奇异点（和它相连的边数量！= 4）
    - 引入点：每个面取中点，和此面所有边的中点连接起来，这样新增了一个点和数条边，
      - 新点的边数和原面边数一致，如果原面是非四边形，则引入了一个奇异点
      - 在非四边形面引入点，一定是奇异点，
      - 引入点后就没有非四边形面了，也就是一次细分后再细分不会增加奇异点了
    - 移动点：
      - 面中间新增的点
      - 边中间新增的点
      - 旧的点
    - 适用于各种网格类型
网格简化：
- 将由三角形面表示的网格，减少三角形数量
- 边坍缩：边的两个顶点合并到新点，边不再存在
  - 坍缩后放在什么位置：边坍缩形成的新点，应放在最优为止（二次误差度量：和周围面距离的平方和最小）
  - 坍缩哪个边：遍历网格体所有边，计算最小二次误差度量，从误差最小的开始坍缩
  - 数据结构：找到当前误差最小的边，并再坍缩一个边后，周围边受到影响要重新计算，用优先队列
正规化：使得三角形面过渡更加平滑

光线追踪

光栅化：实现全局阴影，glossy，全局光照……较困难
光追: 渲染管线默认支持光栅化渲染，可以利用opengl计算着色器自行实现光追，vulkan光追扩展，实现
特点：性能低，效果好
设定：
- 光线
  - 沿直线传播（实则光是波动的）
  - 不相互碰撞
  - 光线可逆性（光从光源出发到物体到人眼，从人眼出发到物体到光源）
- 相机
  - 针孔相机 + 成像平面
步骤
- 准备场景数据
- 光线投射：
  - 对成像平面的每个像素方向，都发射一条光线
- 光线弹射（反射，折射）
  - 找到场景中最近交点：
    - 光线数学表示：射线r(t)：O + td，起点 + 某时间 * 方向（单位） == t时的光线终点位置，向量相加
    - 交点：即在光线上，又在物体表面
    - 光和隐式物体求交：
      - 光和球体求交：
        球体数学表示：(p - c)^2 - R^2 = 0, 球面点到球心的距离的平方 == 半径的平方
        交点满足：(O + td - c)^2 - R^2 = 0，
        求解未知数t，求解一元二次方程，根据求根公式求解
        检查解的合理性
        其中实数（b^2 >= 4ac）有意义，虚数没有意义
        t <= 0没有意义
        没有解，说明相离，光线和球体没有交点
        有一个解，相切，有一个交点
        有2个解，相交，有两个交点，应该选择最近的，也就是t值最小的点
    - 光和显示物体求交
      - 光和网格体求交：
        遍历每个网格，判断是否有交点，最后取t最小的交点
        光和三角形求交：
        方法一：
        光和三角形所在平面求交：
        平面数学表示：(p - p`)*N，任意一点p到平面一点p`形成的向量点乘n==0，也就是垂直
        交点满足：(O + td - p`)*N，一元一次方程求解
        判断交点是否在三角形内：叉乘
        方法二：
        等式左：光线，p0p1p2是三角形3个顶点,p前系数相加==1，
        未知数：t，b1，b2，根据下面的公式求解未知数
        判断交点是否在三角形内：如果3个系数>0，则在三角形平面内
      - 性质：判断一个点在封闭物体内外：如果点在物体内，向任意方向建立射线，交点一定是奇数个，如果在物体外，交点一定是偶数个
    - 光和场景求交
      - for(光线){for(图元){求交，维护最小t值}}
    - 加速求交
      - 光和物体加速求交
        包围盒：把复杂物体用简单的几何体包围起来
        轴对齐包围盒AABB：任意一边都对齐于某个坐标轴
        光和2D包围盒求交
        长方形：2个对线中心区域
        沿每个轴求交：沿着x轴方向，找到光线进入空间的tenter，和离开空间的texit，再沿着y轴方向找到2个t
        光线进入离开长方形的时刻：最后合并为两个线段交集，也就是tenter取最大值，texit取最小值
        判断光和盒体是否有交点：……
        光和3D包围盒求交
        长方体：3个对面的中心区域，通常用左下和右上两个点表示
        沿每个轴求交：……
        光线进入离开长方体的时刻：光线进入了3个对面，则进入盒体，光线离开任意一个对面，则离开盒体,max(tenter), min(texit)
        判断光和盒体是否有交点
        如果texit < 0，则光线在面的背后，则不可能有交点
        如果tenter < 0,texit >= 0, 则光线起点在盒体内，则有交点
        也就是当tenter < texit && texit >= 0 则有交点
      - 光和场景加速求交
        加速求交按空间划分数据结构：四叉树/OCT叉树/kd树/BSP树
        数据结构介绍：详见其他章节
        算法思想：
        划分空间：在光线追踪前
        求交点：
        dfs：
        返回条件：如果和叶节点相交，将其内所有物体，加入到res结果数组，如果光线和盒体不相交返回
        状态转移：否则和子盒体递归求交
        遍历结果数组：如果物体相交，并t值 < 当前最小t，则更新，返回t
        叶盒体大小多少合理：
        如果太稀疏：仍要遍历很多的物体求交
        如果太密：需要和很多很多叶盒子求交
        也就是要控制一个度才能达到最优效果，C~=27 * 物体数量n
        更适用于什么样的物体布局
        物体均匀分布
        算法缺陷：一个网格体在多个叶包围盒内，不能简单的根据物体中心位置决定它在哪个包围盒中，因为这样会忽略某个更近的物体，但如果划分到所有相交的包围盒中，又很难计算，所以一般不用空间数据结构的方式
        加速求交按物体划分数据结构：BVH
        划分空间：按照物体划分
        返回条件：每个包围盒内包含较少物体（比如<5）
        状态转移：找到当前长度最长的维度，找到中位数物体（可以排序 / 算法（215. 数组中的第K个最大元素，用三路快排）），划分为两部分，分解为两个包围盒，对两个子节点递归划分空间
        求交：和上面一样
        注意空间划分：和八叉树不同，不是均匀划分，和kd树不同，不是把物体相切，两个包围盒就像总包围盒一样包裹住各自的物体，这样保证任何物体都在关联的包围盒的内部，就算包围盒间有重叠，也不影响求交
- 像素着色
  - 辐射度量学
    - 在CG中通常使用辐射度量描述光照，因为它给出了一系列度量方法和单位
    - Radiant energy：辐射能量Q，单位焦耳J，辐射出的总能量, 随时间增加
    - Radiant power：辐射通量Φ，单位瓦特W，单位时间辐射出的能量
    - 弧度：弧长/半径，圆周长2Π r / 半径r = 2Π总弧度
    - solid angle立体角: Ω, 单位sr
      - 立体角 = 球面面积A / r^2
      - 总立体角：球体总面积4Π r^2 / r^2 = 4Π
      - 球体大圆周长：2Πr
      - 单位面积（球体坐标系）dA = (r dθ)(r sinθ dΦ) = r^2 sinθ dθ dΦ
      - 单位立体角 dω = dA/r^2 = sinθ dθ dΦ
    - Radiant Intensity：辐射强度I = dΦ / dΩ,在单位时间内，光源会向四面八方辐射能量，往立体角辐射出的能量
    - Radiant Irradiance: 辐射照度E = dΦ/dA, 在单位时间内，物体会从半球方向接收能量，dA接收的辐射能量
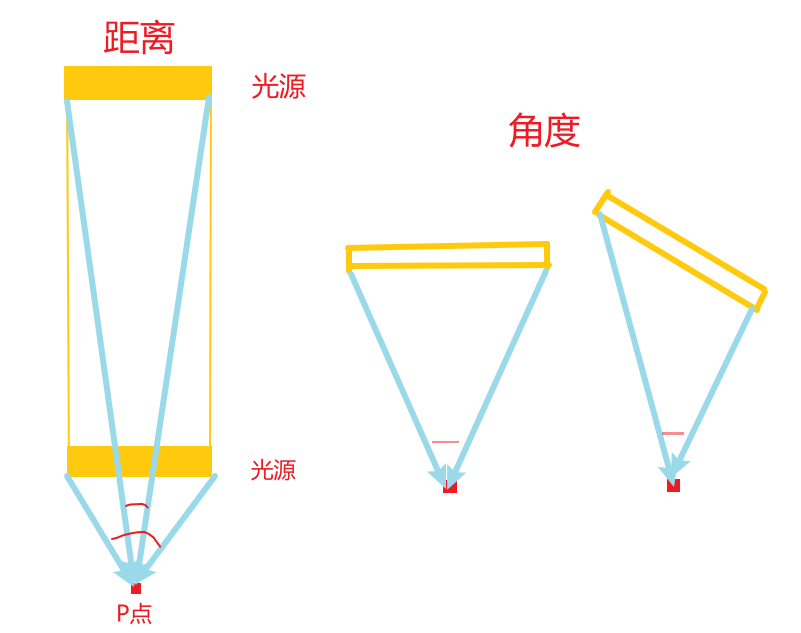
      - A应垂直于辐射方向的表面，因为当不垂直时接收的能量会减少
    - Radiant Radiance：
      - 辐射率：L(p,ω) = d^2Φ(p,ω) / dω dAcosθ
      - p点被着色点，ω表示辐射方向，dω单位立体角、dA单位面积,分子是二次导数
      - cosθ：法线方向和辐射方向的夹角，夹角为90度，说明A于辐射方向垂直，cos为1，不影响A的大小，越平行说明A接收能量的有效范围减少，使得A缩小
      - 可以理解为：
        d²y/da db = d(dy/da)/db
        L = dI / dAcosθ: 从dω辐射的能量，到dA接收的能量
        L = dE / dωcosθ: 从dA辐射到dω的能量，
  - 渲染方程
    - BRDF双向反射分布函数：
      - bsdf = brdf + btdf,因此brdf这里仅考虑反射不考虑折射
      - fr（wi->wr入射->出射）： Lr / Li, 描述了比值关系：反射到某dw的能量Lr / dA从dw接收的能量Li
      - BRDF表示材质，材质是物体和光作用的方式的抽象
      - 漫反射fr：
        假设任何方向进来的光能量一致，因此Li和fi是常量，可以提取到积分外，对cos项积分结果为Π，由于不考虑吸收，根据能量守恒Li == Lo，则fr = 1/Π, 引入光吸收即颜色值p，fr = p/Π
      - 镜面反射fr：
        菲涅尔F：
        F0为基础反射率
        描述反射占比
        绝缘体：通常为非金属，视线和法线越垂直，反射占比多，越平行，反射占比少，折射占比多
        导体：通常为金属，任何视线下反射率都很高
        几何项G：
        微表面模型：从微观角度看物体表面是由一个个微小几何组成，除非绝对光滑
        微表面的自遮挡现象
        法线分布项D：
        GGX：微表面法线和使得wi反射到wo的法线方向一致的比例
    - 反射方程Lr：
      - p点从半球型内所有方向接收的总能量∫Li，反射到lr的总能量∫frLi，cosθi法线和Li的点乘，dwi 积分的标准写法，考虑每个wi入射立体角
    - 渲染方程Lo：
      - 是更接近于物理的光照算法，属于PBR，它考虑反射，不考虑折射，吸收用颜色系数表示
      - 自发光Le + 反射的光
  - 全局光照_光栅化：
    - 直接光照——渲染方程：
      - 一个光源对p点的直接光照仅有wi一个方向，n个光源最多有n条光线对p点提供直接光照，因此求直接光照的话，不需要考虑半球积分，直接遍历所有光源求和即可
      - 结果要色调映射（防止取值被截断）+ gamma校正（颜色是物理的亮度）
    - 间接光照——IBL：
      - 预处理准备：
        IBL：是光栅化实现环境光的一种方式，基于图像的光照，将图像视为光源
        环境贴图：
        获取/生成方式：
        使用资源：较少耗费性能，没有考虑周围场景的影响
        预处理生成: 从原点向6个方向渲染生成环境贴图，考虑周围场景，但这是不正确的，对于不同的p点，受到物体遮挡关系是不同的，都使用原点位置生成的环境贴图，将获得错误结果
        预处理生成: 从每个物体向6个方向渲染生成环境贴图，性能消耗极大，不支持动态场景
        动态生成：每帧从每个物体向6个方向渲染生成环境贴图，性能消耗极大，支持动态场景
        HDR环境贴图资源：
        HDR -> LDR
        HDR：由于PBR基于物理的，光照强度直接使用物理等效值，如果不使用HDR，很多光源被限制到1，无法正确区分相对亮度
        默认缓冲是LDR的，在渲染天空盒这一步，我们在shader中，手动色调映射和gamma校正，使得HDR可以正确转换到LDR纹理中
        存储格式
        RGB 格式：有RGB 3个通道，每个通道8位（可以表示0-255区间，通常映射到0——1）
        存储HDR需要RGB 3个通道，每个通道32位
        RGBE 格式: 是一种高效存储的方式，RGBA 4个通道，每个通道8位，第4个alpha通道存放指数，以便可以用32位存储空间表示HDR数据，不过在使用的时候，需要解析转换为RGB
        环境贴图格式：
        球面映射（用于资产存放（内存开销小），存储高效（转换为ERP，只用一张2D图片存储内存消耗较少），不易采样（环境贴图通常贴到3D物体（球体/立方体）表面，需要知道顶点与uv的数学映射关系），图片失真）
        正常球体展开
        通过鱼眼镜头/3D软件虚拟全景相机拍摄，输出2:1的ERP图片
        等距柱状投影ERP：最广泛使用的简单投影方式，经线映射为等距垂直线，纬线映射为等距水平线，维度较高失真越大
        立方体映射（用于工程使用（采样方便），存储开销大（需要6张纹理），采样方便（根据3D方向），不会失真）
        从ERP到cubemap：
        加载hdr文件：依旧通过stb_image库加载，它会将RGBE格式隐式转换为RGB格式
        渲染cubemap：：创建正方体，放到世界原点位置，对立方体渲染6次，每次对应一个面，根据3D方向（由于位于原点直接使用顶点位置即可），数学转换为2D uv位置，从ERP纹理获取的颜色值作为片元颜色，输出到cubemap的一个面中（也是HDR格式）
        渲染天空盒：详见其他章节，它由于受到摄像机旋转的影响，需要每帧渲染
        辐射度图：
        对环境贴图每个纹素卷积，生成以此方向的半球采样辐射率积分结果，这样预处理，在之后渲染方程使用L项时，直接通过3D方向对辐射度图采样即可（辐照度图不需要每帧渲染，因为它和物体的相对方向不变，假设天空和物体不运动情况）
        渲染辐射度图：
        创建正方体，渲染到世界原点位置，对立方体渲染6次，每次对应一个面
        对半球均匀离散采样，弧度取值区间：Φ从0——2Π，θ从0——1/2Π，这样是半球区间，每次弧度增加Delta，
        根据当前Φθ弧度值，转换为方向向量，
        根据TBN变换，转换到当前片元的切线空间（法线方向用顶点位置）
        结果输出到cubemap的一个面中
        预滤波环境贴图
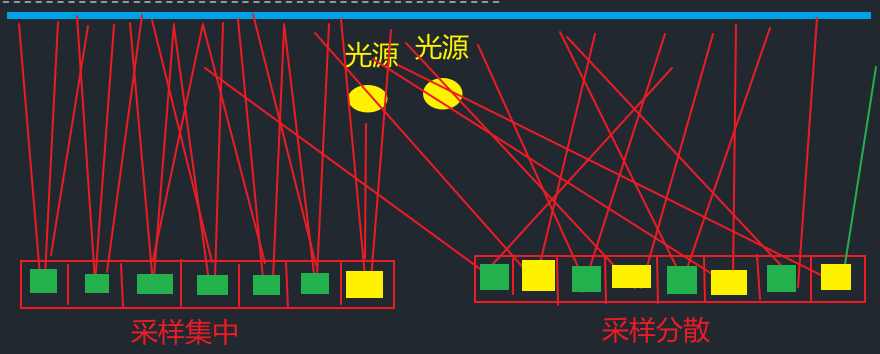
        类似辐射度图，也使用cubemap存储，但考虑了物体粗糙度，物体粗糙度越高，采样越分散，使用mipmap存储，利用glGenerateMipmap函数生成，为了平滑过渡，需要为贴图启用三线性过滤
        N==R==V：镜面反射不同于漫反射，随着观察角度v不同，看到的结果也不同，如果预计算处理，我们无法为所有可能的 V 都预计算一张贴图（BRDF/辐照度），因此只能把v假设为固定值n，也就是假设v和r都为n方向
        低差异序列：xi.x为index/N，范围0——1，均匀递增 xi.y取值范围0——1，生成伪随机样本，比起纯随机样本分布更加均匀
        GGX重要性采样
        生成球坐标
        a = roughness * roughness，则a范围0——1
        方位角 (phi)，2.0 * PI * Xi.x; 球体大圆周长，均匀分割
        天顶角 (theta)的余弦值正弦值
        宽度：cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y)); 当a取值为0，结果为1，当a取值为1，结果为0——1之间，粗糙度越高，范围越大
        高度：sinTheta = sqrt(1.0 - cosTheta*cosTheta); 当a取值为0，cosTheta为1，sinTheta为0，当a取值为1，cosTheta为0——1，sinTheta为0——1
        当a取0绝对光滑时，cosTheta为1，sinTheta为0，转换为笛卡尔坐标永远是(0, 0, 1)指向正y
        当a取1绝对粗糙时，cosTheta为0——1，sinTheta为0——1，转换为笛卡尔坐标，均匀覆盖整个半球
        粗糙度越低越集中到y，粗糙度越高越分散
        由于cosTheta为0——1，sinTheta为0——1，不会超过半球范围
        转为笛卡尔坐标即向量
        转换到TBN切线空间（法线方向用顶点位置）
        up仅用来构建TBN矩阵的，并不是最后的N向量，TBN才是最后的正交基，形成以N即采样方向半球
        N.z趋近于0，说明越接近y（由于把视线假定为n方向，围绕v生成镜面波瓣，也就等于围绕n生成），使用z轴构建，否则使用y轴构建
        取反射向量：ImportanceSampleGGX获得围绕v形成镜面波瓣的反射向量，采样的应该是入射光，这样得知v看到的颜色
        把所有采样结果平均取均值
        mipmap生成：
        要在刚才基础上，外部嵌套循环次数
        glRenderbufferStorage每次缩小mipmap的分辨率和缩小视口大小，这并不会使得渲染区域缩小，渲染区域由P决定，而视口影响图像分辨率（一个图像的采样频率）
        传入的粗糙度值a增大（相当于使用更大范围过滤器过滤，将产生更模糊的图像）
        访问可以指定mipmap等级采样（可以是小数）
        优化：
        贴图接缝：
        成因：
        正常来说，随着a的增大，过滤范围越大，图像越模糊，边界过渡越自然才是，为什么随着a的增大，接缝越明显呢？
        我们知道当纹理分辨率和屏幕分辨率不一致，想要找到屏幕像素对应的uv坐标，需要启用过滤
        但是对于立方体贴图，没有面与面之间的过滤，只能在一个面中过滤，比如采样一个面边缘位置不能和其他面中的临近像素过滤，发生不正确的过滤，因此会形成边界
        当粗糙度高，较低级别的mipmap有更少的分辨率，因此更有可能发生不正确的过滤，使得接缝出更明显
        可以启用GL_TEXTURE_CUBE_MAP_SEAMLESS，以便在立方体面间支持双线性插值
        亮点：
        成因：
        环境贴图上有非常明亮又占比较小的光源，有的像素采样到就会变得很亮，有的没有采样到又很暗，采样到的像素在图像中形成一个个亮点，
        当a越低，采样范围越集中，要么完全不触及光源，要么完全触及光源，不容易临近像素高频变化，当a越高，采样越分散，临近像素容易高频变化
        在生成预滤波环境贴图时，不再直接采样源环境贴图，而是glGenerateMipmap() 生成它的一系列mipmap，根据a动态计算level去从对应的mipmap采样辐射度
        当粗糙度越大，GGX的结果越小，pdf值越小，样本立体角增大，样本立体角/源立体角增大，level增大，从更高等级的mipmap采样
        使用高级别mipmap，使得原来小而明亮的点，转为大而亮度降低的点，这样消除了原来明亮的噪点
        BRDF积分图：
        横轴是NV点乘，纵轴粗糙度，颜色值为BRDF值
        分解BRDF项
        首先将F菲涅耳项提取出来，
        根据公式把F项展开
        用a替换(1−ωo⋅h)^5项
        将F项变换
        把积分拆分成两部分，
        用(1−ωo⋅h)^5替换a
        Fo是常量可以提取到积分外
        积分依旧通过GGX重要性采样
        f项为G因为（F提取了，D在重要性采样里），ωo⋅h就是NV点乘
      - 漫反射
        直接光照值 + 间接光照值——漫反射（F项是常量，L项直接采样）
      - 镜面
        直接光照值 + 间接光照值——漫反射 + 间接光照值——镜面反射
  - 全局光照_光线追踪：
    - 全局光照：直接光照（直接到达物体，没有经过弹射） + 间接光照/环境光（1次及以上光线弹射）
    - 渲染方程设定：
      - 忽略渲染方程自发光项
      - 渲染方程的积分项用蒙特卡洛——采样法求解,蒙特卡洛包含3项（f(x),n,p），f(x)对应LFcos这3项——被积函数
      - 如何采样：采样数量n项自定义的(例如100)，最简单方法为均匀采样，则p项 = 1/n
    - 直接光照——渲染方程：
      - 定义Lo，发射n条光线，如果光线打击到光源，Lo+=计算结果，如果没有打到光源，Lo+=0
    - 间接光照——路径追踪：
      - 定义Lo，发射n条光线，如果光线打击到光源，Lo+=计算结果，如果光线打到了物体，Lo+=递归计算结果（相当于作为光源，即Li项）
      - 返回条件：如果和场景没有交点 / 超过最大弹射次数
    - 优化算法复杂度：
      - 比如每个物体发射100条光线，每根光线都打到物体，这些被打到的物体又要发射100条光线，这样变为了10000条光线路径……
      - 这样会发生指数级爆炸，为n^bounces次，n为采样次数，bounces为弹射次数
      - 当n==1时，1^bounces = 1，始终为1条光线路径，这样就防止了指数级爆炸
    - 减少噪声：
      - 每个像素随机发射n条光线，SPP每个像素采样次数，将这些光线结果取平均颜色值
    - 俄罗斯轮盘赌注：
      - 现实场景中光弹射无数次，如果限制了它的最大弹射次数，将会造成能量损失
      - 轮盘赌注：以一定概率p发射光线，并将结果/p，以1-p概率不发射光线，结果为0
      - 此时期望为Lo（离散），它达到了数学期望的能量守恒（并非物理的）
    - 减少噪声：
      - 黑色/暗色噪声：成因：在半球区域完全随机采样时，对于较小的光源很难打击到，返回0颜色值
      - 解决方式：
        增加SPP，但这样消耗太多性能
        向光源有偏采样，如果新增有偏向光源方向采样的光线，这样不会消耗太多性能，做法就是改写渲染方程
        采样范围/定积分域：从半球区域采样变为光源区域采样，∫A……dA
        考虑光源并非垂直于法线：dA将发生变化，和光源距离和角度有关
        定义Lo，向光源发射一条光线，如果中间没有阻挡物（从p点向光源发射ray，和场景求交，如果交点距离<\p到光源的距离，则说明有阻挡物），Lo+= 有偏渲染计算结果,俄罗斯轮盘发射1条光线，如果光线打到了物体，Lo+=递归计算结果
    - 总结：

Games101

本文由作者按照 CC BY 4.0 进行授权

几何

光线追踪

热门标签