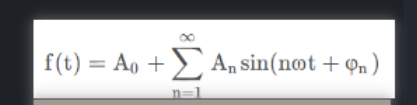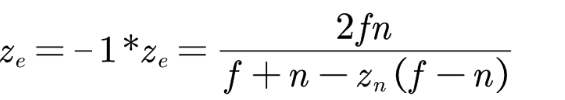101复习(3`光栅化，傅里叶变换，深度测试，着色、坐标转换)

发表于 2025/09/03

作者 senlongan

20 分钟阅读

光栅化

光栅化遍历每个图元为它们生成片元
采样法：遍历屏幕内每个像素中心的采样点，进行覆盖性测试，利用叉乘判断是否在图元内部
优化：根据顶点确定包围盒范围，仅遍历包围盒范围内的采样点
Aliasing走样问题：锯齿，摩尔纹（moire Patterns）（水波纹），车轮效应（分不清顺逆时帧旋转）……
抗锯齿：SSAA,MSAA,FXAA,TAA……详见其他章节

傅里叶级数变换

周期函数
- 函数：y = f(x)
- 周期函数：若存在一非零常数T，对于定义域内的任意x，都有f(x)=f(x+T) 恒成立，则f(x)叫做周期函数，T叫做这个函数的一个周期，形如正弦、余弦
- 振幅：从最高点到最低点的距离除以2
- 相移: 函数水平向右移动多远
- 垂直位移：函数垂直向上移动多远
- 频率：1/周期
- y = A sin(Bx + C) + D
  - 振幅是A
  - 周期是2π/B
  - 相移是−C/B
  - 垂直移位是D
数列和级数
- 数列：以非负整数集为定义域（每项用f（x）表示，x>=0）的一列有序（随着x递增f（x）的顺序）的数,每一个数都叫做这个数列的项，著名的数列有斐波那契数列，杨辉三角……
- 级数：将数列的项依次用加号连接起来的函数
- 函数项级数：将函数项依次用加号连接起来的函数
- 三角级数：将三角函数（正弦余弦）项依次用加号连接起来的函数
傅里叶级数展开：微积分中的函数展开方法之一
- 三角级数展开：
  - 展开式：
    - 把一个f(t)以t为周期的非正弦函数，用一系列以t为周期的sin函数，组成的级数表示
      - ω = Π/l，周期T = 2l，l = T/2，
      - 直流分量：常数项
      - 谐波次数：n
      - 一次谐波：求和部分，n==1称为一次谐波，n==2时称为二次谐波
      - 常数系数：Ai φi
  - 周期映射推导：
    - 按照三角公式展开
    - 再一系列替换
    - 再替换x,即g(x)
      - 将x + 2Π，
      - 常数项不变
      - cos(n(x+2π))=cos(nx+2nπ)=cos(nx)
      - sin(n(x+2π))=sin(nx+2nπ)=sin(nx)
      - 因此满足g(x+2Π) = g(x)
      - 这就把T为周期的三角级数转换成以标准2π为周期的三角函数,这样方便统一方式计算
  - 三角函数系的正交性：
    - 三角函数系：1,cosx,sinx,cos2x,sin2x,⋅⋅⋅,cosnx,sinnx,⋅⋅⋅
    - 区间[−π,π]上正交：指在三角函数系中，任何不同的两个函数的乘积，在区间[−π,π]上的积分等于零，两个相同函数的乘积，在区间[−π,π]上的积分等于Π
  - 傅里叶系数公式推导：
    - 将左右同时积分，根据三角函数系的正交性，等式右端除第一项外，其余各项均为零，由于在-Π——Π对常量c的积分=2Π*C，因此可以转为乘法形式，移项得，这里少写了积分符号
    - 左右积分并同时*cosnx，等式右端除k=n的一项外，其余各项均为零，根据三角函数系的正交性结果为Π，移项表示an
    - bn同理，左右同时*sinnx
  - 傅里叶级数收敛；
    - 周期为2π的函数f(x)，如果在周期可积，那么一定可以作出f(x)的傅里叶级数
    - 傅里叶级数是否能收敛（n趋近于无穷函数结果）？是否一定收敛于函数f(x)？函数需要满足以下条件——狄利克雷条件：
      - 在一个周期内连续或只有有限个第一类（左、右极限都存在，第二类间断点至少有一个极限不存在）间断点(函数在xi时不连续)
      - 在一个周期内至多只有有限个极值点
    - 当x是f(x)的连续点时，级数收敛于f(x)
    - 当x是f(x)的间断点时，级数收敛于1/2[f(x^−)+f(x\^+)],左极限右极限的算数平均值
  - 傅里叶级数展开示例：
    - 由于函数有有限个第一类间断点，由收敛定理得到收敛于0
    - 根据不定积分求值方法，可以得到anbn结果
    - 将傅里叶系数带入函数得到傅里叶级数
  - 正弦级数和余弦级数
    - 也有一些函数的傅里叶级数只含有正弦项/只有余弦项，这时由于函数奇偶性有关的
    - 偶函数关于y轴对称，基函数关于原点对称
    - 当f(x)为奇函数时，f(x)cos nx是奇函数，f(x)sin nx是偶函数，故an==0
    - 当f(x)为偶函数时，f(x)cos nx是偶函数，f(x)sin nx是奇函数，故bn==0
傅里叶级数变换：把一个函数经过复杂变换为另一函数，还可以逆变换为原函数

深度测试

作用：3D-遮挡关系
深度值计算时机：在NDC空间获得每个顶点的深度值，在光栅化阶段为所有生成片元，根据重心插值计算片元深度值
深度值存储：计算完成将存储在寄存器中，供之后适用
透视校正后z值为(n+f)/2的点会挤向n还是f？通过具体值带入方式，求得物体向f移动
什么叫做非线性深度值？近处物体的距离/深度值差异较大，远处物体的距离/深度值差异较小
非线性->线性推导
- 思想：现在使用的是NDC映射到0——1范围的深度，是一个非线性深度，将它转换到视图空间下，使用此空间的深度进行计算，即为线性深度
- 正向看：
  - e->c：设透视投影矩阵第3行最后两项为AB，则视图坐标Aze + Bwe = zc裁剪坐标，由于视图空间中we为1，转换为Aze + B = zc，wc = -ze
  - c->n：zc/wc = zn，将zn用ze表示(Aze + B)/-ze = zn
- 反向看：
  - 深度->n：深度值0——1，转换到-1——1的NDC空间，只需要*2-1
  - n->e：已知zn = (Aze + B)/-ze，那么移项可得ze = -B / (zn + A)，已知AB带入此公式可得图中公式，已知zn即可求得ze
  - 计算线性深度：(z - n) / (f - n)
非线性深度作用：
- 深度测试：像素深度值用有限精度的浮点值存储，近处物体深度值差异加大，减少深度冲突，远处物体由于在画面占比较小，减少深度值差异
线性深度作用：
- 需要3D位置信息
深度缓冲：有一定分辨率，每个像素存储float类型深度值，范围在0——1之间，深度越近越接近0黑，越远越接近1白
默认深度测试（必须）：发生在fs之后，根据比较规则和寄存器中的深度信息更新深度缓冲（可读写）
提前深度测试（可选）：发生在fs之前，Early-Z深度测试依赖于上一次drawcall的late-z的结果，不会更新深度缓冲（只读），将未通过深度测试对应的片段丢弃
- 优势：让未通过深度测试的片段不必fs计算
- 注意：Early-Z不会更新深度缓冲，默认深度测试的存在是必须的
  - 开启Alpha测试
  - 假如有2个物体ab，a为完全透明，b不透明，且b在a后，先渲染a，预期结果为呈现b
  - 如果只存在late-z：
    - ab覆盖的片元都被fs计算，Alpha测试后a未通过丢弃，b通过，与预期结果相符
  - 如果只存在early-z并允许更新深度缓冲：
    - 丢弃b片元，保留a，fs：计算a片元颜色值，Alpha测试：丢弃a，结果ab都被丢弃，和预期不符
  - Early-Z不更新深度缓冲，late-Z更新深度缓冲
    - Early-Z：深度缓冲区初始为1.0，ab通过Early-Z，fs：计算a片元颜色值，Alpha测试：丢弃a，late-z：b通过，与预期结果相符
深度冲突
- 由于深度缓冲的精度有限，可能会发生深度值相同的情况，此时会造成画面闪烁
- 解决方法
  - 尽量不要物体靠太近
  - 使用更高精度的深度缓冲
  - 近平面设置远一些，近处精度高

着色

原理
- 光和物体的作用方式：散射（反射（漫反射，镜面反射），折射），被吸收的颜色，微表面方向、自遮挡……
- 颜色：未被吸收的物体颜色传入人眼，使得我们看到物体颜色
- 反射：
  - 笼统角度：漫反射向周围四面八方反射，镜面集中在一个镜面波瓣的反射，通常物体越粗糙越接近于漫反射
  - 微观角度：物体越粗糙，微表面越不平整，光线反射方向偏差大，微表面越平整，光线总是趋近于同一方向反射
- 高光：镜面反射由于光线反射的聚集性，亮度很高
- 阴影：光的直线传播中被物体阻挡，从而照射不到的物体形成阴影
- 夹角：光线方向和法线方向夹角越大，物体接收到的光能量就越小，颜色越暗
- 各项异性材质：微表面存在一定的方向性
- 能量守恒：光线传播越远每个角度的能量越小
Blinn-Phong着色模型(近似模型)
- 视线方向v，光线方向i，法线方向n，光源位置l，着色点位置o，物体颜色c，反光度s/粗糙度a……其中inv为单位向量
- 未被吸收/物体颜色：设定为常量
- 不考虑折射，阴影……
- 间接光照：设定为常量
- 漫反射：Ld = kd(I/r^2)max(0,i*n); 吸收 + 接收 + 反射，kd表示未被吸收的颜色，I为光线强度，r为光与点的距离，0限制到0——90°，不考虑从平面下方照射
- 镜面反射：Ls = ks(I/r\^2)max(0,n*h)^s, 吸收 + 接收 + 反射，ks表示未被吸收的颜色，
- 半程向量h：
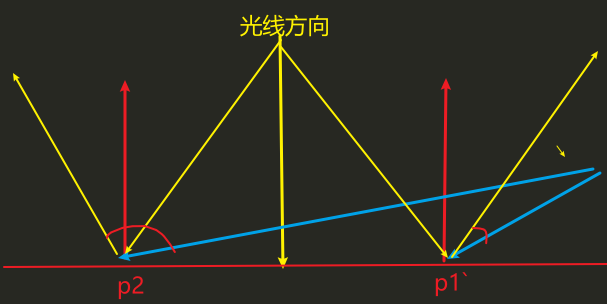
  - 断层成因：v和wi都在平面上方，但p2点没有正确着色（这里并不是指突然从高亮变为0）
  - 指数反光度s：通过cos得到-1——1的结果，会受到s的影响，虽然总体取值不变，角度只有非常接近0°时，结果才会为明显>0的值，否则结果都非常接近0，当s值越大时，这种变化越明显，控制高光范围（明显>0的范围）越小，亮度变化越剧烈
  - 粗糙度大断层越明显：s值越小，高光范围越大，在图像中占据很大的范围
  - 解决方法：
    - 原本比较v和r，如果vr都在平面上方，夹角范围0——180°
    - 现在比较n和h（v+i的单位向量，vi两个方向的平分向量），如果vi都在平面上方，夹角范围0——90°，这样没有约束到0的情况
  - 要注意：
    - 如果视线在下方，没有问题，因为默认会开启背面剔除，就算着色了也看不到
    - 如果光线在下方，也是有可能h和n在同侧，这样计算出不正确的结果，对于解决此问题，首先应该判断wi是否和n同侧（夹角<90度），如果非同侧则应约束到0
  - 特点：由于从0——180°夹角范围约束到了0——90°范围，那么在相同s的情况下，nh夹角通常比vr夹角更小，相同p点亮度更高，亮度变化不剧烈，高光范围更广，因此可以增大s反光度，来达到和冯氏光照一样的效果
投光物：
- 上述把光源假设为空间中的一个点，但现实生活中光源并非一个点，通常是有体积的
- 向着色模型一样，依旧对真实光源做近似简化处理，把光源分为3类
- 平行光：
  - 模拟太阳光，由于太阳距离我们极远，每条光线近似于平行，我们假设它是平行光
  - 因此光照入射方向对任何p点都一致，不在需要向量减法去获得入射方向
- 点光源
  - 模拟灯泡，假设光源从一个点向四周均匀发射光线
  - 衰减模型：
    - r^2：
      - 非线性，物理真实，
      - r距离
      - I光照强度/r^2
    - F = 1.0/Kc+Kl∗d+Kq∗d^2：
      - 非线性，经验模型，方便调参应用不同衰减效果，
      - 常数1保证保证分母永远不会比1小，一次项线性，二次项非线性，kck1kq是系数根据d距离查表确定
      - I光照强度 * F
- 聚光灯
  - 模拟手电筒，假设光源从一个点向锥形区域均匀发射光线
  - 聚光强度：
    - 定义聚光所指方向，指定切光角, 落在这个角度之外的物体都不会被照亮
    - 如果光源和物体的向量和聚光所指方向的夹角 < 切光角，则说明点在聚光灯范围内，被照亮
    - 软化：定义ϕ（内光切）γ（外光切），如果在内圆锥内，强度为1，在内外圆锥的差集部分做渐变处理，强度为0——1，在外圆锥外，强度为0
    - 对于渐变部分：I = (θ−γ) / ϵ, θ是光源和物体的向量和聚光所指方向向量的点乘结果，y是外光切的点乘，ϵ 内光切点乘-外光切点乘，I聚光的强度
着色频率
- 按顶点，像素根据顶点的fs结果插值，开销更小，效果略次
- 按像素，像素根据顶点的数据插值，用fs计算，开销更大，效果更好
- 两种方式顶点数量越多，效果越好