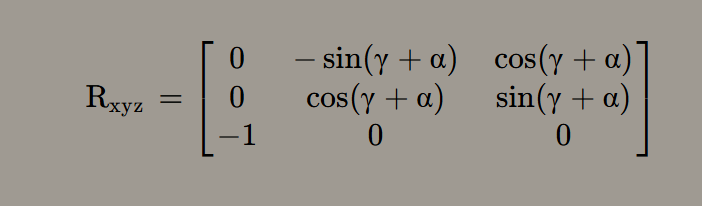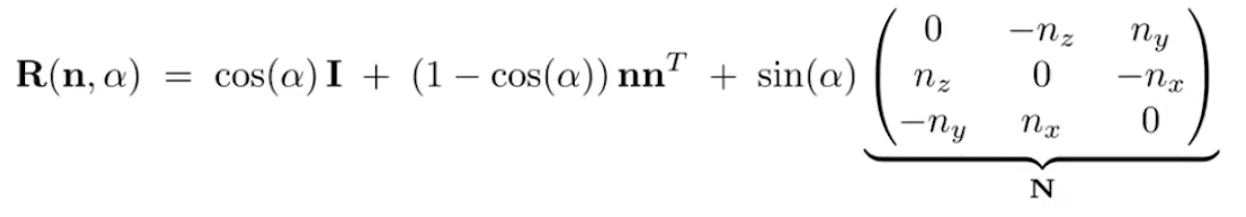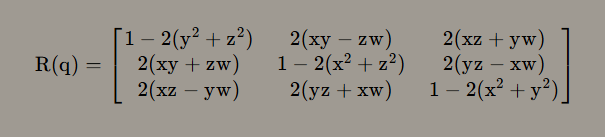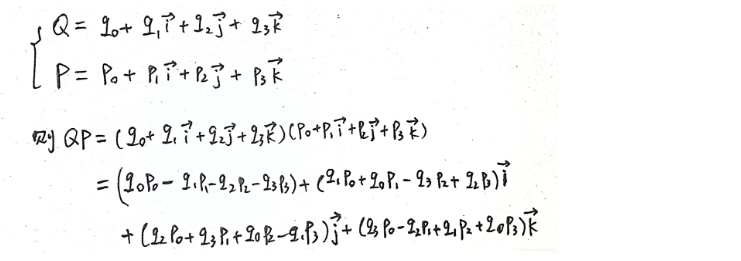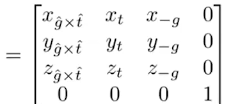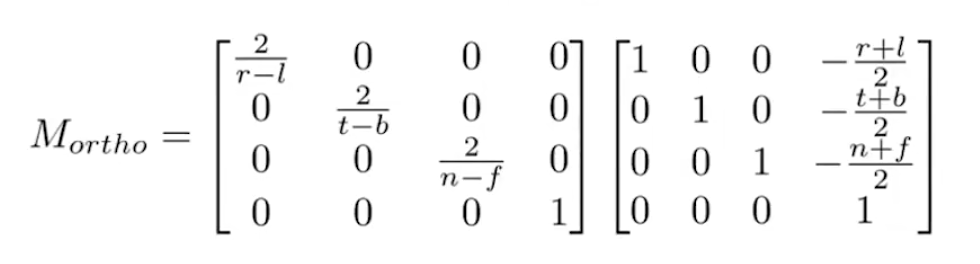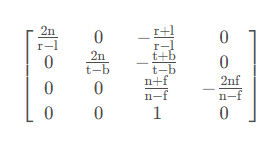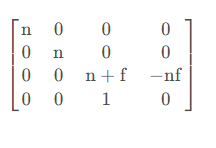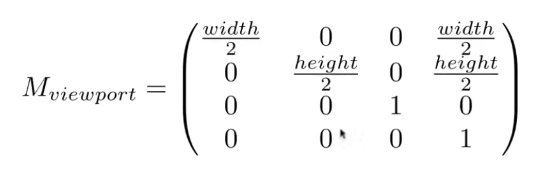101复习(2`变换)

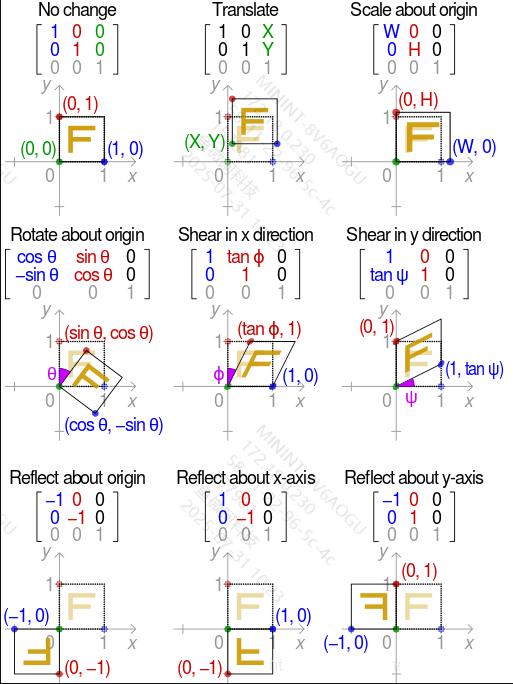
变换

• 仿射变换:
  • 
  • 线性变换和平移变换的组合
  • 包括:旋转，缩放，位移,翻转,切变, 反射，错切……
• 线性变换
  • 缩放
    • S1 * x, S2 * y, S3 * z
  • 旋转
    • 
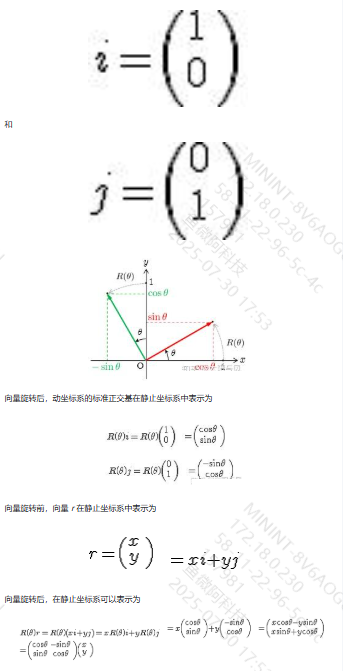
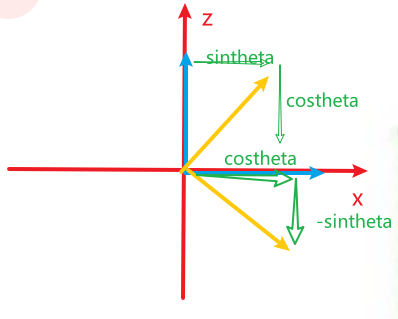
    • 2D旋转矩阵推导（只能绕虚拟z轴旋转）
      • 两个单位向量ij，旋转矩阵为R(θ)
      • 用R(θ)旋转两个单位向量，根据三角函数得到旋转后的向量
      • 向量r可以用ij表示
      • 注意：图中cos(θ)sin(θ)并不是标注的虚线，是虚垂线点到原点的那段距离
      • 问题：如果使用非单位向量例如（0,2)，(2,0)去推导，是否R(θ)的结果不同
        • R(θ) * （0,2) == 2 * R(θ) * （0,1)，仍然可以利用单位向量推导，最后通过2缩放向量长度，这样R(θ)结构不变
    • 欧拉角——旋转算法：
      • 欧拉角旋转算法将绕任意旋转轴旋转，分解三次旋转, 每次绕世界坐标系的一个轴旋转，根据一定顺序，例如：XYZ，ZXY，YXZ……
      • 
      • 由于三次旋转变换也是矩阵表示，矩阵乘法不遵守交换率，因此不同的顺序会形成不同的复合旋转矩阵，上图是ZYX的顺序，欧拉角为α，β，γ的复合矩阵
      • 其中三次旋转的角度pitch俯仰、Yaw偏航、Roll翻滚为欧拉角
    • 3D旋转矩阵推导（可以绕无数个轴旋转）
      • 
      • 
      • 绕哪轴旋转哪轴值不变
      • 根据右手螺旋定则建立2D坐标系：另外两个非旋转轴，按照xyz的优先级，从一个轴到另一个轴
        • 绕 X 轴旋转时，Y 轴向右，Z 轴向上
        • 绕 Z 轴旋转时，X 轴向右，Y 轴向上
        • 绕 Y 轴旋转时，X 轴向右，Z 轴向上
      • 确定旋转角度方向：从旋转轴正方向看的逆时针方向
      • 旋转矩阵是正交矩阵
    • Gimbal——船体陀螺仪：
      • 由三层嵌套的圆环（每个圆环有2个连接头（相当于坐标轴）和内侧相连），旋转轴，转子（具有质量增加惯性）
      • 当船体发生了摇晃，哪个圆环连接头线段 和旋转轴平行，则此圆环绕旋转轴旋转，如果有外环带动外环旋转，无论怎样摇晃，旋转轴永远和世界坐标系的y轴平行
      • 作用：旋转轴永远和世界坐标系的y轴平行，作为定轴参考，可以实时测量船体的姿态，保证风浪中的稳定性
    • Gimbal——万向节死锁：
      • 当船体发生了剧烈摇晃，90°，某一个圆盘的连接头线段将和另一个连接头线段平行
      • 例如，船体绕x旋转90°（中环旋转），外内连接头平行，这时绕z旋转，由于没有和旋转轴平行的连接头线段，则失去了自身调节能力，旋转轴不再和世界坐标系的y轴平行
      • 本质：机械结构，内环旋转影响外环轴旋转，当旋转90/-90度时，发生轴重叠
      • 船体问题：陀螺仪发生万向节死锁，导致船体测量功能短暂失灵
    • 欧拉角——万向节死锁：
      • 
      • 触发条件：当按照某种旋转顺序形成的复合矩阵，其中第二个欧拉角为±90度时，发生万向节死锁
      • 结果：绕z旋转和绕x旋转是等效的（α，γ）（也可以想象为轴重叠），失去自由度（β）
      • 误区：发生死锁并不意味着这种状态无法通过欧拉角表示出来，空间中的任何状态都能通过欧拉角变换得到，只是某些状态表示不唯一而已
      • 影响：获得非预期结果
    • 罗德里格斯——旋转算法
      • 
      • n是旋转轴，a是旋转角度
    • 四元数——旋转算法
      • 复数：a + bi（实数+虚数）
      • 四元数：q = w + xi + yj + zk（复数的扩展），w实部，xi + yj + zk虚部，ijk为虚数单位
      • 四元数表示：
        • 复数式：w + xi + yj + zk
        • 齐次形式：（w,x,y,z）/ (w,v)
        • 矩阵表示:
          • 
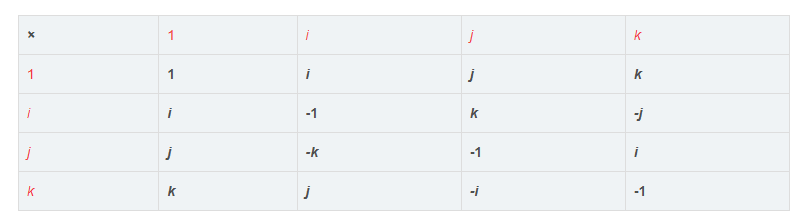
      • 四元数运算：
        • 乘法：得到一个新的四元数
          • 
          • 
      • 四元数计算旋转：
        • 定义旋转轴 v =（vx, vy, vz），旋转角度θ = 弧度制, 被旋转向量w = (wx, wy, wz)
        • 表示四元数：q =（cosθ/2，sinθ/2 * vx，sinθ/2 * vy，sinθ/2 * vz）
        • 表示四元数的共轭：q^-1 = （cosθ/2，-sinθ/2 * vx，-sinθ/2 * vy，-sinθ/2 * vz）
        • 被旋转向量的四元数形式：qw = (0, wx, wy, wz) = 0 + wxi + wyj + wzk
        • 应用旋转：qw` = q * qw * q^-1
        • 新向量的四元数形式：qw` = (0, wx`, wy`, wz`) = 0 + wx`i + wy`j + wz`k
        • 新向量非四元数形式：w` = (wx`, wy`, wz`);
    • 欧拉角 vs 四元数：
      • 欧拉角：
        • 优点：直观；可表示>180度的旋转
        • 缺点：万向节死锁，插值不平滑，旋转顺序重要性
      • 四元数：
        • 优点：计算效率高，解决万向节死锁, 插值平滑，内存消耗小
        • 缺点：不直观，不可表示>180度的旋转
• 平移变换
  • 位移：
    • x + L1, y + L2, z + L3
  • 齐次坐标：为n维的点引入n+1个分量，值为1，使其支持平移变换
• 模型变换顺序
  • SRT->TRSV
• 视图变换
  • 摄像机由一个坐标系确定它的位置和旋转，其中原点e为摄像机位置，t对应up轴，g为lookat轴，t*g对应正交轴，轴方向为旋转方向
  • 物体的每个点(x,y,z)应用摄像机的逆变换，即逆矩阵
  • 平移：x + -ex, y + -ey, z + -ez
  • 旋转: 先求出点到摄像机的变换，逆矩阵即反方向变换，其中逆矩阵==转置矩阵
    • 
• 投影变换
  • 正交
    • 
    • 定义裁剪空间tblrnf
    • 获取空间中心坐标，将空间中心对齐世界原点
    • 压缩为标准立方体：一个数 * 它的倒数 = 1
  • 透视
    • 
    • 定义平截头体nf，垂直fov，水平fov（视野）
    • 投影矩阵
      • 
      • 投影矩阵推导
        • 
        • 先从垂直视野的侧面看，由于相似三角形原理，对于空间中一点（x,y,z），连接原点和近平面交点（x`,y`,z`），y`/y = n/z（n即z`），同样对于水平视野的顶部看，x`/x = n/z
        • 可以得知空间中一点在x和y方向，被挤压后的位置，
        • 由于为了接下来计算方便，让每个分量*z
        • 可以得知投影矩阵的前两行，和第四行
        • 我们知道当z==n时，挤压后仍然为n，由于刚才每个分量*z，这里n * z即n^2,同样对于远平面上的一点，挤压后仍为f，f * z即f^2
        • 设第3行为00AB，由于和xy无关前两个元素为0，近平面点应用变换后得到n^2（为了今后/w透视除法时统一），根据2元1次方程组可以解得值
    • 正交矩阵……如上
    • 变换到-w——w的齐次裁剪空间
• 透视除法：
  • 由于上述*z简化操作，获得-w——w的裁剪空间，我们应/w也就是/z，这样变换到NDC空间
• 视口变换
  • 屏幕分辨率：像素多少
  • 
  • z不变，因为我们只关心xy在屏幕空间的坐标，乘法将-1——1拉伸到宽高，加法使得左下角对齐坐标原点，变为屏幕空间
• 空间变换：
  • 局部空间 -> M(SRT) -> 世界空间 -> V -> 观察空间 -> P -> 裁剪空间 -> /w -> NDC空间 -> 视口变换 -> 屏幕空间
• 真实步骤（以上有些步骤为了方便理解，有说的不准确的地方）
  • 透视矩阵（带入法）：xyz均匀放大，转换为齐次形式，齐次空间
  • 正交矩阵：均匀压缩齐次空间
  • /w：对于zview越大，xy越小（近大远小），近平面点不变*n/n，对于z，物体非线性的靠近f（非线性深度）
  • -w——w的空间，w = -zview，那这个zview使用的哪个点的zview？每个点的zview，-w——w是针对每个点的空间