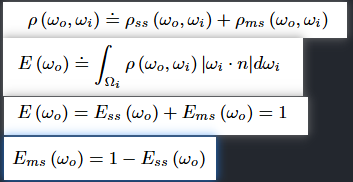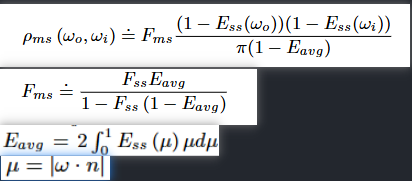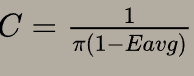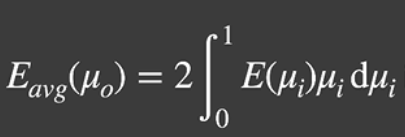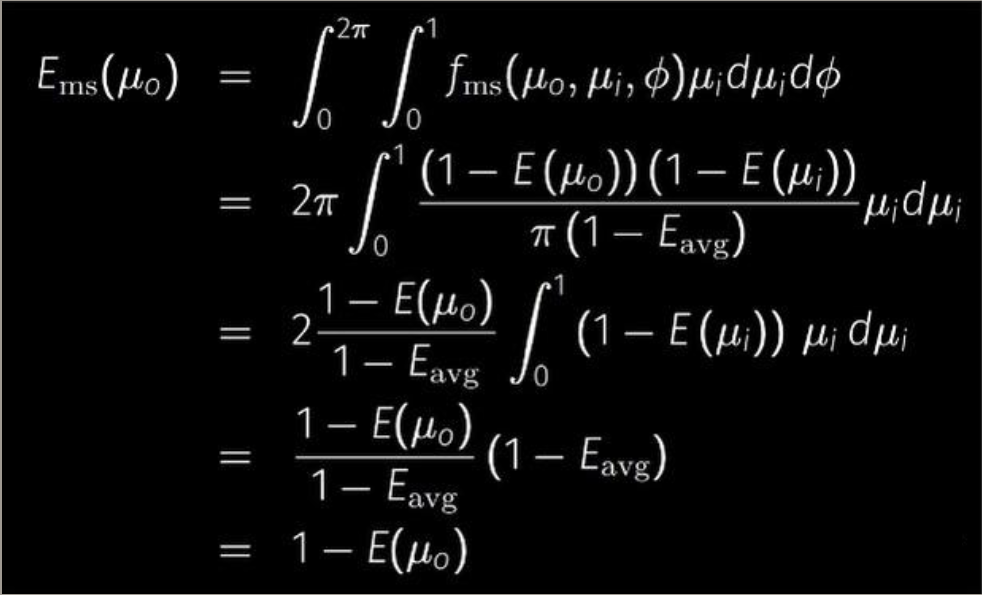Games202(8`第10章)

第10章

BRDF

FDG项：详见其他章节

---

注：以下是论文的描述，在games202课程中，由于很多符号都表达的不一致，就统一按论文中符号来说

---

The Kulla-Conty Approximation

Single scattering单次散射ss，Multiple scattering多次散射ms

对于BRDF的D项（通常使用GGX算法），只考虑了光线ss的结果，没有考虑经过ms到达人眼的情况（将它直接丢弃掉），这样引起能量损失

当粗糙度越高，丢失的能量越多，结果越不正确，和正确的效果差异越大（GGX在a==1时，能量损失达到约60%，当使用其他算法GTR/STD，它甚至会变得更糟，达到90%以上）

Heitz (2014) 考虑新的BRDF模型，我们之前的BRDF模型作为pss单次散射出射的能量（wi->wo），新增了pms多次散射出射的能量（wi->wo），pms作为单方向能量补偿项

考虑半球所有方向，总的出射能量E（wo）

它也分为Ess和Ems两个部分组成，Ems作为总能量补偿项，Ems为∫pms

我们没有考虑吸收，因此根据能量守恒，所有入射能量都被反射回来,E（wo）= 1

Kulla & Conty (2017) 近似方案,是一种精确度明显较低，但更简单，更快速的解决方案，它建立在假设材质是各项同性（同性指所有方向均相同，异性指在方向上有差异）的基础上

fms考虑了菲涅尔吸收（吸收即颜色项）

由于BRDF的可逆性，它分解为入射和出射两个方向的ss丢失，ss丢失即作为ms需要补偿的部分

u是换元，这个图片是games202中的推导

分母是用来归一化的常量c，它的推导如下（当不考虑fms时，对pms的积分也就是Ems，应该==1 - Ess）：

这是games202推导可以参照，fms==pms，uo==wo，ui==wi，最后结果为1 - Ess