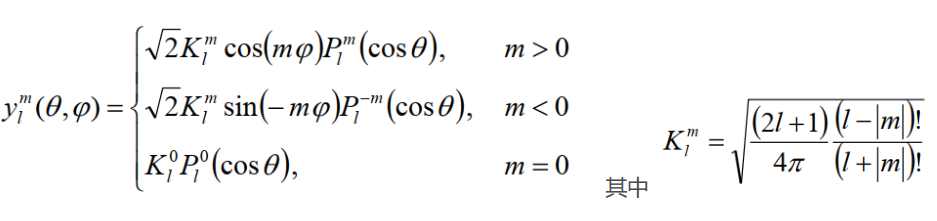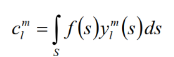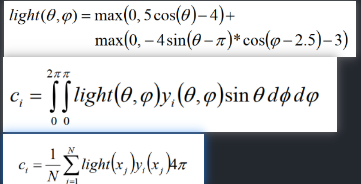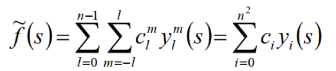文章

Games202(3·作业1，第6章)

发表于 更新于
作者 senlongan
17 分钟阅读

作业1

首先作业框架为我们绘制了场景，但是无阴影效果：

1736590619431

这是包含阴影的PBR 公式: V + L + B

1736655532337

框架解析：

  • engine.js: 新增了一个人物模型，1个地面模型
  • webglrender:
    • 新增了shadowMeshes数组
    • render中，变为了两次pass，首先为场景（使用阴影材质）渲染阴影mesh，然后为场景渲染颜色
  • 平行光：（本次使用平行光而非点光源作阴影）
    • 网格体
    • CalcLightMVP: 返回光源的MVP
  • shadow材质 继承主材质：
    • 包括FBO的帧缓冲区，为了存储阴影相关数据的，
    • 包括lightMVP 光视角的MVP
    • 函数: buildShadowMaterial 构建阴影材质
  • FBO.js，这个类的构造首先创建帧缓冲和设置属性，创建纹理和设置属性，纹理和缓冲关联，以及错误检查，解绑
  • shadow glsl：（为场景渲染一张深度图）
    • pack函数的作用是把一个(0,1)的float值储存到RGBA四个通道中
    • gl_FragCoord是内置的视口变换后的坐标:其大小范围是x：[0, ScreenWidth]，y：[0, ScreenHeight]，z：[0, 1]，返回它即返回深度值

JAVA语法

constructor（）{ super（……）； } 是构造函数，super部分是调用基类构造函数

阴影steps：

  • 将world pos（经过model）* LightMVP矩阵变换到光空间，获得NDC[-1,1]标准化设备坐标
  • 为了获取在光屏幕下的纹理坐标，通过/w（视口变换）-> 在+1/2映射到[0,1]（因为纹理是0，0->1，1）
  • 判定阴影：根据 当前depth（纹理坐标.z） >= map保存的值（texture2D采样），就返回0判定为阴影，否则返回1

普通阴影：

  • 修改CalcLightMVP函数，
    • 写出light MVP矩阵，
    • 根据传入进来的参数SRT，构建Model矩阵，
    • 根据光源属性构建view矩阵，
    • 根据视锥体的左右上下近远，创建投影矩阵
  • 完善glsl中的useShadowMap函数，
    • 查询当前着色点在ShadowMap上记录的深度值，并与转换到light space的深度值比较后返回visibility项，
    • 首先获取阴影贴图中的值，获取当前的深度值，如果当前 >= map保存的值，就返回0判定为阴影，否则返回1
  • 修改phong glsl中的main
    • 首先获取SM上的纹理坐标
    • 调用useShadowMap返回visibility的值
    • 让最后颜色返回gl_FragColor = vec4(phongColor * visibility, 1.0);

1736667896409

自遮挡:

有两种方法解决子遮挡，我们用自适应的方法

1736671443331

根据这个公式，我们添加一个getShadowBias函数，如图所示，

  • A = （1 + 取整（在uv上的过滤半径大小））* （平截头体大小 / （阴影贴图大小 * 2））
  • B = 1 - dot(法线，光线方向)
  • Bias = 常数 * AB

修改useShadowMap函数，cur_depth - bias >= depth

1736671464792

pcf：

让shaderpoint和shadowmap一圈的范围比较，获取平均值

  • 写fs中的pcf函数，
    • 为了优化性能，使用poissonDiskSamples生成随机种子保存在poissonDisk数组中，作为offest位置，采样NUM_SAMPLES指定次数次，最后+=求和的结果求平均值，
    • 其中filterRadiusUV过滤半径取：FILTER_RADIUS / SHADOW_MAP_SIZE得到uv（0–1）中的大小
    • 这里有一点注意的地方，useShadowMap（）应放在pcf（）的上面，否则会调用失败

1736671481108

pcss：

步骤如下：

  • STEP 1: avgblocker depth，找到平均block深度在findBlocker（）中计算
    • 首先确定在shadowmap中应该采样的区域，它和3个参数有关
      • 光的大小（越大，block范围越大）
      • 近平面距离shaderpoint的距离（距离越远，block范围越大）
      • 光到shaderpoint的距离有关（距离越远，block范围越小）
    • 然后在此范围内像pcf一样随机采样，取block平均值
  • STEP 2: penumbra size，根据课上的公式计算penumbra过滤系数（即filterRadiusUV）（其实可以理解为，近处pcf程度低，远处pcf程度高）
    • float penumbra = (zReceiver - avgBlockerDepth) * LIGHT_SIZE_UV / avgBlockerDepth;
  • STEP 3: filtering，调用pcf函数即可，使用penumbra过滤系数，对pcf的过滤范围缩放，也就是penumbra的值越大，取样的offest越大，从而形成更模糊的效果

可以看到随着 遮挡物和被投射物的距离越远，越趋近软阴影

1736675710806

模型旋转：

首先设置rotate的初始值和需要传输和调用的参数

*//数据修改

  • 在engine
    • setTransform函数中添加模型变换_旋转部分，这是修改顶点数据（负责初始时应用的旋转）
    • Add mesh中设置模型旋转初始值
  • Mesh.js中也加入旋转，以便可以接受模型的初始旋转变换
  • MeshRender.js中CameraParameters中添加旋转，要让相机接受模型的旋转数据
  • //平行光MVP
  • DirectionalLight.js
    • 修改灯的顶点数据，虽然灯不用变换位置，但灯也用到了setTransform参数需要传入参数
    • 也需要更改CalcLightMVP生成的光照矩阵，添加rotate部分, 以便传入模型的mvp
  • //材质
  • PhongMaterial
    • 构造添加rotate参数，因为在这里会调用CalcLightMVP
    • buildPhongMaterial也添加rotate参数
  • 同样在ShadowMaterial中也如PhongMaterial
  • loadOBJ.js中调用创建材质时，传入参数

实时：

为了随时间增加旋转角度，需要在mainloop中获取deltatime： 然后在render中接受时间，并让网格体旋转矩阵

实时阴影

SM的渲染正是在渲染更新中，因此是每帧都会重新渲染

可以看到模型在旋转，模型旋转我们更改了顶点数据，以及glsl中的model矩阵

但阴影没有变，是因为我们没有向shadow glsl中传入旋转后的模型，

光源旋转

  • 灯光要实时旋转，还要更改灯光的MVP，

多光源

  • 首先为光源添加lightIndex编号
  • 在engine中创建新光源
  • 在WebGLRenderer中，需要将所有光源渲染结果叠加，要开启混合gl.enable(gl.BLEND);

第6章

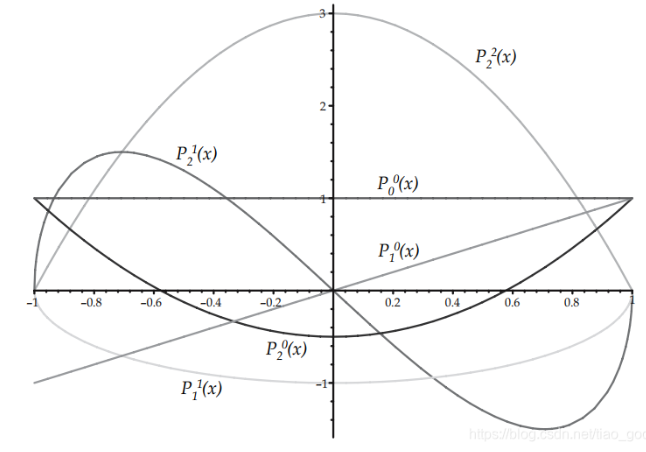
勒让德多项式

  • 代数式：由字母和数字组成，并由运算符号连接的式子
  • 单项式：由数或字母的积组成的代数式
  • 多项式：有限个单项式的线性组合
  • 正交多项式：将单项式乘积进行积分时，如果它们相同，结果为常量，如果它们不同，结果为零
  • 勒让德多项式
    • 1737558031198
    • 用于将定义在[-1,1]区间函数fx展开，它同傅里叶展开一样都是正交多项式
    • 勒让德公式
      • 1737558031198
      • m: 次数，整数，满足 0 ≤ m ≤ l
      • l: 阶数，非负整数
      • x: 自变量，在区间 [-1, 1] 内
    • 计算勒让德函数
      • 求l阶n次多项式（输入m<=l），自变量x时的f(x)值
      • 根据公式1首先求Pm^m
      • 根据公式2求Pm^m+1
      • 根据公式3，循环求解，它依赖 l-1 和 l-2

SH球谐函数

  • SH也是函数展开的一种方式，但它的基函数定义在球坐标系中，用于对三维空间中的函数进行展开，比如球面函数（即x定义域为球面）（球面的参数化：用球坐标表示球面上的每一个点）
  • 基函数：
    • 计算l阶m次，在theta和phi球坐标下的y(θ，φ)
    • 1737558031198
    • P：勒让德多项式
    • K：规范化函数的比例因子
    • l: 阶数，非负整数
    • m：次数，整数，[-1, 1]
  • 基函数可视化：
    • 1737558031198
    • 当3维SH函数被可视化成几何体时,向每个球坐标采样获得结果值，几何体的形状由结果值的绝对值确定，表面的颜色由结果值的正负性确定，绿色为正值，红色为负值，
  • 投影：
    • 1737558031198
    • 投影：计算l阶m次基函数的系数c，将原函数f和sh的l阶m次基函数积分，积分域取决于f的定义域，比如球面函数的定义域为球面
    • 示例：
      • 1737558031198
      • 原函数light
      • 系数ci为l和y的积分，积分域为球体，sin：赤道附近的片段比极点周围的片段对最终结果的影响更大
      • 解积分：蒙特卡洛：采样使用均匀采样(θ，φ)，pdf（1/4Π），则w为1/pdf = 4Π，其中被积函数为l*y
  • 重建：
    • 1737558031198
    • 重建：每个系数和对应的基函数相乘，再求和，获得原函数的近似函数f`(x)
    • 越高阶重建效果越接近，但会带来更大的存储压力、计算压力，甚至摩尔纹现象，通常使用3阶就可以获得99%的效果
  • 球面函数可视化：
    • 遍历经纬度，count取决于像素ij的数量
    • 根据球坐标获取对应的重建值
    • 存放到数组对应位置中，以便作为纹理输出
  • 特性：
    • 标准正交性：
      • 如果两个sh基函数yiyj，i为第一个函数的lm对，j为第二个函数的lm对，如果i==j，乘积积分返回1，否则返回0
    • 旋转不变性：
      • 对原函数fx经过R旋转后获得gx，重建获得gx的系数 == 对原函数fx的系数应用系数旋转矩阵M（n * n）来得到gx的系数，由于基函数不依赖于fx，则旋转后不需要改变基函数，因此不考虑它
      • 比如将光源（光源函数==原函数）旋转后，想要获得新的重建的近似函数，并不需要重新计算，系数变换就可以
      • 系数旋转矩阵：
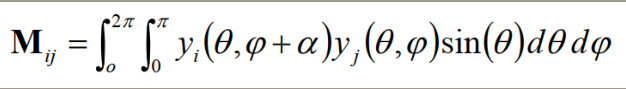
        • 1737558031198
        • Mij = 每个元素都是通过旋转y与非旋转的y积分来计算的
        • 1737558031198
        • 这是绕z旋转的2阶旋转矩阵，让gx的系数构成的列向量左乘这个矩阵，即可获得旋转后的系数
        • 如何表示任意旋转呢？同欧拉角的思想一样，可以用一系列简单的旋转表示复杂旋转
        • 1737558031198
        • 任意旋转可以绕x旋转1次，绕y旋转1次，我们已经有了绕z的矩阵，绕y用xzx表示
        • 但上述的计算复杂度特别大，由于矩阵的稀疏特性，我们可以降低它的复杂度，但仍很耗费性能
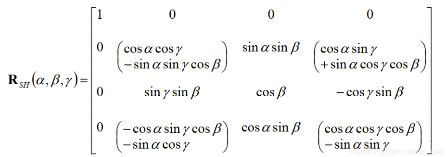
        • 1737558031198
        • 可以预计算，把这5个矩阵相乘组合，获得统一的矩阵，从而加快运行时计算的速度，但当阶数高时，表达式会变得极其复杂和庞大，并且由于使用欧拉角，它会出现万向节锁定问题
        • 1737558031198
        • 有个技巧可以既避免万向节锁死，又可以加快计算速度，我们利用标准3*3三维旋转矩阵的对称性，根据这些恒等式，避免了上面5个矩阵相乘的运算，当sinβ=0时，这个公式就失效了，可以利用下面的R矩阵，以及恒等式
  • 标准示例：
    • sh核心优势是快速解多个函数的乘积积分，比如渲染方程
    • 假设渲染方程有L和V项两项乘积积分
    • 普通复杂度为N即采样次数
    • 将两项分别重建用近似函数表示，两项乘积积分，即每个对应的函数（系数*基函数）相乘，再求和，由于正交性，基函数i==j乘积==1，则可以化简掉，只保留系数乘积，复杂度为M即函数个数个
  • SH函数的笛卡尔版本
    • 1737558031198
    • 1737558031198
    • 从球坐标表示转换到笛卡尔坐标表示，由于基函数不依赖于fx，因此它是固定的，这个为2阶的SH函数的笛卡尔版本
    • 这样在3维直角坐标系中一个点xyz，可以投影在上面的基函数，计算sh系数
Games202
实时渲染
本文由作者按照 CC BY 4.0 进行授权
本页总访问量次