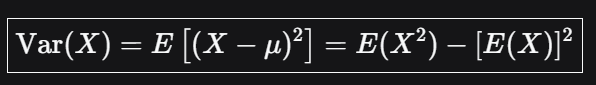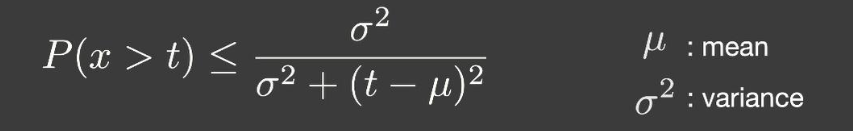Games202(2·第4章，第5章)

第4章

vssm方差软阴影映射

pcss在1、3步，对一定范围内的像素一个一个比较，求得结果，这非常耗费性能，vssm通过快速估计一定范围内的结果值，来优化性能，这个估计需要利用均值和方差

求均值：

范围查询：

• mipmap：
  • 查询方式：预计算不同分辨率下的纹理，记录不同大小正方形范围的值
  • 查询形状：只能正方形查询
  • 精度：结果近似
  • 速度: 非常快
  • 存储：增加原图1/3的存储
• SAT：
  • 查询方式：根据前缀和思想（详见其他章节），四次采样，布尔运算，范围内的总和 / 个数 = 均值
  • 查询形状：任意矩形
  • 精度：结果准确
  • 速度：较快
  • 存储：增加和原图等大的纹理

求方差：

数学公式：

这里xi是shadow map中存储的depth值，利用范围查询，可以快速得到区域平均值 == 期望 == E^2(X)

额外生成一张图，每个像素存储depth^2，可以快速得到区域平均值 == E(X^2)

求概率

pdf即正太分布函数，根据均值和方差找到横坐标，横坐标划分的（1-左边面积）就是概率

这个面积可以通过cdf得到，C++ 中的函数ERF函数可以计算cdf

也可以使用切比雪夫不等式，近似求得结果，但是有一个苛刻的条件：t 必须在均值右边

求解

对于平均dblocker：

其中两个比例可以利用切比雪夫不等式求解

总区域内的平均深度可以利用mipmap / SAT 求解

假设非遮挡物的平均深度 = shading point的深度

这样只剩下一个未知数，也就是要求得的结果

对于PCF：

可以利用mipmap / SAT 快速求得均值

问题

vssm做了很多大胆的假设，那么在实际偏离假设情况，就会出现不准的现象

假设深度值是正太分布的，如果实际不是正态分布，就会出现漏光和过暗的结果，为了解决这个问题，使用更高阶的moment(矩)

第5章

SDF

SDF有向距离函数

SDF（p） 是一个函数，它接受空间中的任意一点p作为输入，并返回该点到某个物体表面最近的距离，返回值用正负性来表明该点位于物体的内部还是外部

几何体混合

有两个物体的SDF，将两个SDF混合操作，得到新的SDF，即新的几何体，可以很好的把几何进行过渡

Ray Marching光线步进：

详见其他章节

基于sdf的软阴影：

• 步骤
  • 预处理：
    • 为场景中的静态物体预计算（在CPU中）sdf，存储为3D纹理
    • 3D纹理生成：AABB包围盒将整个场景包裹住，离散分割为一个个小格子即体素，用体素中心点p计算sdf(p)和整个场景的最近距离作为体素值，计算sdf(p)需要遍历每个物体的sdf取min
    • 3D纹理坐标左下前角是 (0,0,0)，右上后角是 (1,1,1)
    • 对于动态物体，可以使用更高级的技术（如DFAO）
  • 延迟着色：
    • 几何阶段获取G-buffer
    • 光照阶段
      • 执行Ray Marching
        • 计算阴影：
          • 如果p点位于阴影，则获取世界空间位置
          • 步进方向：朝向面光源上随机或特定采样点的方向
          • 步进长度：p点映射到3D纹理中某个位置，利用3线性插值计算sdf均值
          • 安全角：
            • 
            • 每次步进过程取sdf为半径做圆，圆切线和步进方向夹角为安全角，取最小的角度作为总的safe angle
            • 
            • 我们知道p到p1距离作为斜边，sdf（p1）作为对边，用反余弦arcsin可以根据边长比求得夹角，但是它的计算量很大
            • sdf（pi）* k /（pi-p），k越小,半影区域越大,越接近软阴影效果，K越大,半影区域越小,越接近硬阴影效果
            • safe angle越小，越趋近于硬阴影，safe angle越大，越趋近软阴影
        • 光照计算：光照值 * 安全角（作为衰减指）
• sdf得到高质量软阴影方法，昂贵存储开销，高昂预计算成本

Global Illuminace

IBL：详见其他章节