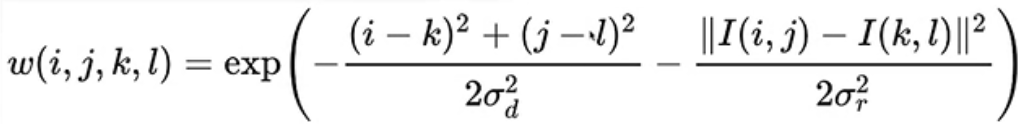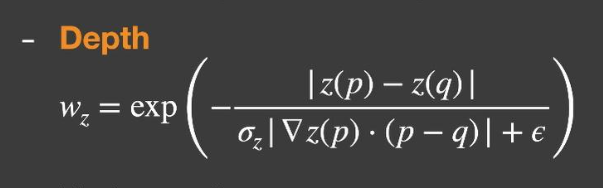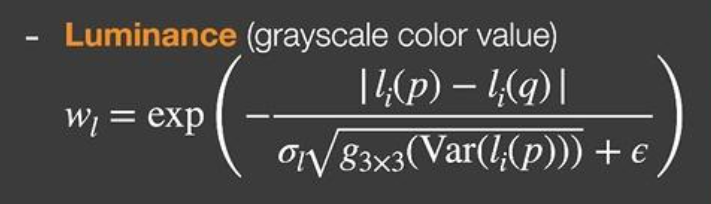Games202(10`第13章、第14章)
第13章
规定:
~C未降噪图片
—C已降噪图片
k->kernel滤波(卷积核)
卷积伪代码:
- 对于每个像素i,找到周围的像素j
- 加权:对每个像素j,会根据绝对距离和标准差求得j权重,通过j值 * j权重 得到j对i的贡献值,sum +=
- 平均:循环结束,i值 = sum_值 / sum_权重(未归一化需要除法)
高斯滤波—空间降噪
使用高斯滤波核:详见其他章节
权重值:绝对距离越大,权重越小
效果:整体模糊,边界不清晰,相当于去除高频信息,但没有考虑高频信息是否是噪声,低频信息是否有噪声的问题
双边滤波——空间降噪
如何模糊,但边界仍然清晰?可以对边界和非边界做不同处理
如何判定边界:颜色值的差异
权重值:颜色差距越大,权重越小,绝对距离越大,权重越小
权重的计算公式:
i和j代表中心像素位置,k和l代表当前像素位置
I(i,j)表示中心像素的颜色值,I(k,l)表示当前像素的颜色值
左边项是绝对距离影响,右边项是颜色影响
联合双边滤波——空间降噪
考虑更多的特性:比如坐标,颜色,法线,深度……
对于权重的计算会考虑所有特性,去计算贡献(权重),将贡献合并,得到最后的权重值
优化方法
逐渐增长的过滤
原本每个像素做N*N的采样,如何减少采样次数?
每次过滤范围扩大,filter过滤器样本数为N*N,样本间隔2^i(i从0开始)
比如做5层,样本数为5*5,对于第5层,间隔为2^4 = 16,采样索引-32 -16 0 16 32,相当于64*64的filter
原本需要4096次采样,现在变为5*5 *5 = 125次采样,获得近似结果
离群值删除
使用filter处理噪点(过亮/过暗的像素)会有问题,过亮的地方会更亮,解决方法就是在过滤之前先去除噪点,那如何确定哪些是噪点?如何处理呢?
step:
- Detection探测:对每个像素计算一定范围内的均值和方差,如果当前的像素在 均值 +- 方差的范围外,则判定它为噪点
- Clamping限制:将这个噪点颜色值限制到 均值 +- 方差 的范围内
第14章
SVGF时空方差引导滤波——时空降噪
结合联合双边滤波的特性混合的思想,与TA的时间性
深度:
- exp(x)是返回以e为底的指数,由于指数是-x,则x越大结果越小
- 分子部分是两者的深度差值,深度差异越大,贡献越小
- 标准差用来控制指数衰减的快慢的参数
- (深度的梯度(沿着法线方向)* 两点间的距离)避免错误判断,例如对于侧向面观察深度差异大贡献小,但同面理应贡献大,所以应考虑的是A和B在平面法线垂直方向上的深度变化
- e避免深度相同造成分母0,避免差距太小导致最后的数值太大
法线:
角度差异(0——180)越大点积结果越小贡献越小,
但是结果有可能是负值(夹角 > 90度),使用max()把负的值给clamp到0,表示没有贡献
标准差用来修改点乘结果变化速率,越大变化率越快
颜色:
- 和深度公式很像,不同的就是sqrt这个部分
- 和离群值删除思想类似,为了避免采样到噪声,利用中心点的标准差,来获得正确的贡献,噪声会带来大的差异,贡献减小
- 时间累计:求出i帧variance方差,和i - 1帧的variance混合
其他过滤方法
Recurrent AutoEncoder (RAE)循环自动编码器
是深度学习模型,它结合了自动编码器和循环神经网络的特点,将G-buffer和noisy图输入,将temporal的结果累积起来
AutoEncoder,是一个漏斗形的结构,形状很像一个U字形,因此也可以称之为U型神经网络,每层都有往返的链接,因此可以复用上一帧遗留下的信息而不是通过motion vector查询
高级抗锯齿
TAA时间域抗锯齿
和emporal accumulation 时间累计——时间降噪方法原理差不多,用来解决锯齿问题
Enhanced subpixel morphological AA 增强型子像素 形态学抗锯齿
建立在 MLAA(形态学抗锯齿)算法之上,图像方法会先去识别它,然后通过各种匹配的方法(每种形状模式预计算了一张查找表)找到它正确结果的样子
Deep Learning Super Sampling(DLSS)深度学习超级采样
借助深度学习神经网络,将一张低分辨率的图输入最后得到一张高分辨率的输出
2.0版本摒弃了通过神经网络猜测的结果,而是更希望去利用temporal的信息
其中不能使用clamp解决一些问题,因为最终要的是一个增大了分辨率的图,如果此时我们用上一帧的结果盲目的clamping势必会因为一些小的像素的值是根据周围的点的颜色猜测出来的,而且猜测的值很像周围的点,也就是我们得到了一个高分辨率的图但是很糊
因此我们需要一个比clamping更好的复用temporal信息的方案
工业界技术
Tiled Shading平铺着色
虽然利用Deferred Shading可以仅对可视网格计算光照,但是这些网格仍要遍历所有的光源进行计算,很多情况下并不是每个光源都能影响到这个片段(点 / 面光源),因此仍做了很多无用的光照计算
- 将屏幕分成了若干个小块,每个切出来的小块对应场景中3D的区域
- 对每个面光源或点光源计算出立方体 / 球体的覆盖区域
- 在像素着色时,会找到对应场景中3D的区域被哪些光源覆盖,只会用这些光源光照计算
Clustered Shading集中着色
我们不仅将屏幕分成了若干个小块,还要在深度对其进行切片,因为如果只分成若干个小块区域的话,区域内的深度可能会十分大,光源不一定会对根据深度细分后的网格有贡献,因此排除了更多的不必要光源
Level of Detail (LOD)多层次细节
根据物体与相机的距离,动态地调整物体的细节程度,从而优化渲染场景性能的技术,LOD的难点在于不同层级之间的过渡,可以使用blending的方法实现手动平滑过度
- mip-map texture的多级渐远纹理,不同分辨率的纹理
- Cascaded shadow maps级联阴影映射,不同的SM分辨率
- Cascaded LPV级联式线性参数变化
- geometric LoD,顶点数量数量不同,高模和低模