6·一维操作（双指针，滑动窗口、二分查找）

双指针

• 有l，r两个指针，可同向，反向移动
• 同向——快慢
  • 有l，r两个指针，都指向0
  • 当f->next不为空，一个快一个慢移动
• 反向
  • 有l，r两个指针，分别指向0,n-1 左右端
  • 当l < r时，每次根据条件选择l++还是r–
• 使用场景：一维数组，搜索/判断/调整……问题

滑动窗口

• 对于非固定大小窗口
  • 有l，r两个指针，都初始到0
  • 当r < n时，每次根据条件选择l++还是r++
• 固定大小窗口
  • 有l，r两个指针，l初始到0，r初始到某位置
  • 当r < n时，每次l和r同时++
• 使用场景：一维数组，连续子串，子数组问题

二分查找

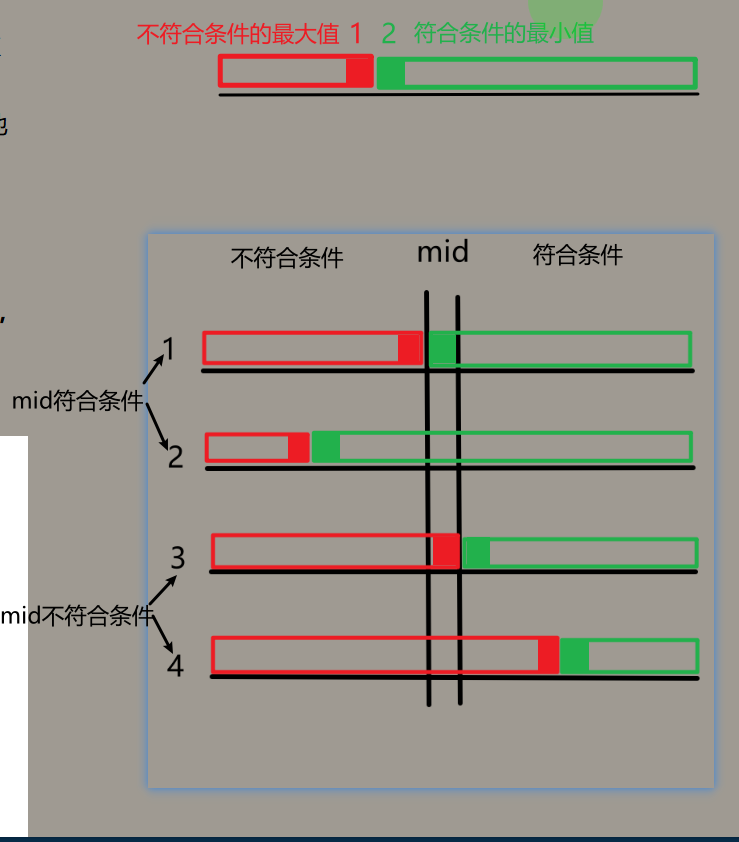
• 适用条件：对排序/部分排序数列, 找到符合条件的最小值/不符合条件的最大值 问题
• 算法思想：首先lr确定左右边界，每次check(mid)根据mid是否符合条件，确定排除的数列和保留的数列
• 边界问题：循环条件是否有=号，mid取值是否+1，判断条件是否有=号，划分区间mid是否需要+-1，结果返回谁……

• 二分模板：

  while (l<=r)
  {
    int mid=(l+r)/2;
    if (check(mid))
    {
        ans=mid;
        r=mid-1;
    }
    else l=mid+1;
  }
  

  展开

  • 用ans记录结果，循环条件(l<=r)，表示l>r时循环停止

  //找到符合条件的最小值
  while (l<r)
  {
    int mid=(l+r)/2;
    if (check(mid)) r=mid
    else l=mid+1;
  }
  //找到不符合条件的最大值
  while (l<r)
  {
    int mid=(l+r+1)/2;
    if (check(mid)) r=mid - 1
    else l=mid;
  }
  

  展开

  • 结果是lr都可以，(l<r)，表示l==r时循环停止
    • 
    • mid取值问题：
      • mid取(l+r)/2，找不符合条件的最大值问题，会出现死循环
      • mid取(l+r+1)/2，找符合条件的最小值问题，会出现死循环

  //传统方法
  while (l<=r)
  {
    int mid=(l+r)/2;
    if (a[mid]==key) return mid;
    else if (a[mid]>key) r=mid-1;
    else l=mid+1;
  }
  return -1;
  //ans方法
  while (l<=r)
  {
    int mid=(l+r)/2;
    if (check(mid))
    {
        ans=mid;
        r=mid-1;
    }
    else l=mid+1;
  }
  return (ans != -1 && nums[ans] == target) ? ans : -1; 
  //找到符合条件的最小值
  while (l<r)
  {
    int mid=(l+r)/2;
    if (check(mid)) r=mid
    else l=mid+1;
  }
  return (nums[l] == target) ? l : -1; 
  //找到不符合条件的最大值
  while (l<r)
  {
    int mid=(l+r+1)/2;
    if (check(mid)) r=mid - 1
    else l=mid;
  }
  return (nums[l] == target) ? l : -1; 
  

  展开

  • 查找特定值问题, 可以转为 把>=target作为符合条件 / 把<=target作为不符合条件
    • 判断条件:把>=target作为符合条件,当mid==t应该应该移动r，把<=target作为不符合条件，当mid==t应该应该移动l
• 总结：
  • 左闭右闭代表的就是[left,right]的区间，区间内部包含目标值，循环条件l<=r，mid取值(l+r)/2，判断条件t<=mid移动r，划分区间l=mid+1,r=mid-1，结果如果有ans返回ans，否则需要判断==情况并返回，通用
  • 左闭右开代表的就是[left,right)的区间，区间内部包含目标值，循环条件l<\r， mid取值(l+r)/2，判断条件t<=mid移动r，划分区间l=mid+1,r=mid，结果返回l/r，用于找到符合条件的最小值
  • 左开右闭代表的就是(left,right]的区间，区间内部包含目标值，循环条件l<\r， mid取值(l+r+1)/2,判断条件t<\mid移动r，划分区间l=mid,r=mid-1，结果返回l/r，用于找到不符合条件的最大值
  • 遵守上述方式，否则有可能出现找不到正确结果/死循环问题