4·算法复杂度、排序算法

发表于 2025/07/29 更新于 2025/10/18

作者 senlongan

19 分钟阅读

算法复杂度分析

性能测试：在编写程序后算法性能测试，精确性高，算法编写好运行，依赖数据规模
算法性能分析：在编写程序前对算法性能估计，精确性低，使用方便
算法复杂度与数据规模之间的增长关系，它并非实际执行时间/存储空间（具体数值），而是反应一种趋势（n相关的表达式）
四则运算
- 加：平行
- 乘：嵌套
- 减：去掉平行
- 除：去掉嵌套
化简：
- 每句指令执行时间均设为1
- 用常数1取代运行时间中的所有加法常数
- 除最高阶项以外，其它次项和常数项可以忽略
- 与最高次项相乘的常数可以忽略
渐进记号：
- Θ，读音：theta、西塔；既是上界也是下界(tight)，等于，平均情况复杂度
- Ο，读音：big-oh、欧米可荣（大写）；表示上界(tightness unknown)，小于等于，最坏情况复杂度
- ο，读音：small-oh、欧米可荣（小写）；表示上界(not tight)，小于
- Ω，读音：big omega、欧米伽（大写）；表示下界(tightness unknown)，大于等于，最好情况复杂度
- ω，读音：small omega、欧米伽（小写）；表示下界(not tight)，大于
平均情况复杂度：把所有情况需要的时间相加 / 所有情况个数
均摊时间复杂度：一个算法某次操作的时间比较高，这次操作时间，需要将其均摊到其它操作上，
- 比如执行n次，每次复杂度是1，最后一次，复杂度是n，总共是2n，2n / n次，每次操作的平均耗时为1
常见的时间复杂度T(n)
- O(1):算法执行时间不会随着数据量改变
- O(logn)：满足logx^n次的循环
- O(n): 一层循环
- O(nlogn): logx^n次的循环，嵌套一层循环
- O(n^2): 二层循环
- O(n^3): 三层循环
空间复杂度S(n)
- O(1): 变量
- O(n): 一维数组
- O(n^2): 二维数组

排序算法

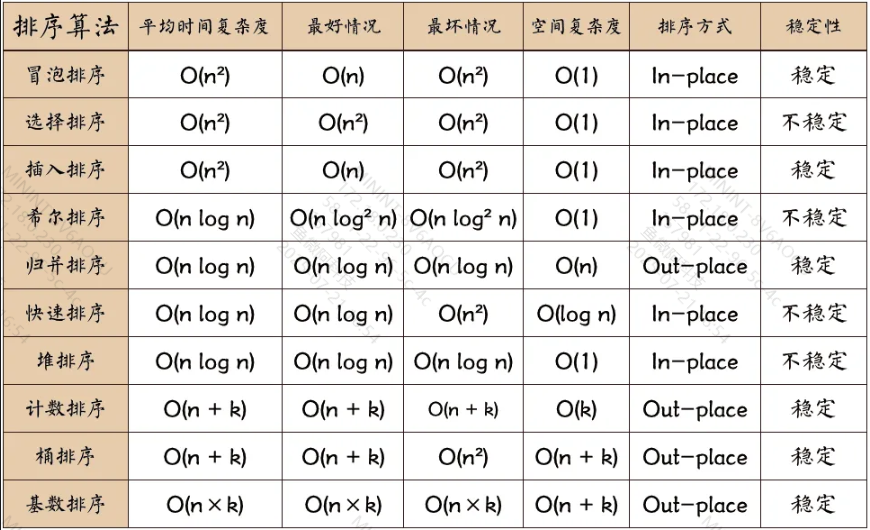
算法复杂度

In-place：原地算法，不占用额外内存
Out-place：非原地算法，占用额外内存
稳定性：对于序列中相等元素，排序后相对位置不变，则认为是稳定的
k：对于计数：k 是待排序数组中元素的最大，对于桶：“桶”的个数，对于基数：k 是基数通常为10

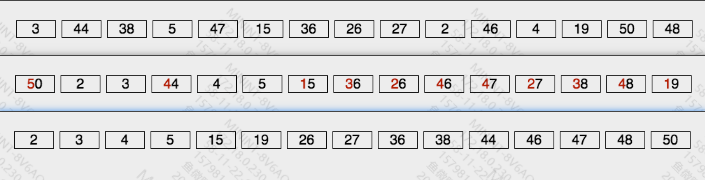
冒泡排序（Bubble Sort）（比较排序）

  #include <iostream>
  using namespace std;

  void bubbleSort(int arr[], int n) {
      for (int i = 0; i < n - 1; ++i) {
          bool swapped = false;
          for (int j = 0; j < n - i - 1; ++j) {
              if (arr[j] > arr[j + 1]) {
                  swap(arr[j], arr[j - 1]);
                  swapped = true;
              }
          }
          // 如果没有发生交换，说明数组已经有序，提前退出
          if (!swapped) {
              break;
          }
      }
  }

  int main() {
    const int n = 9;
    int arr[n];
    for(int i = 0; i < n; i++) {
      cin >> arr[i];
    }
    //BubbleSort(arr, n);
    //SelectionSort(arr, n);
    //InsertionSort(arr, n);
    //MergeSort(arr, 0, n - 1);
    //QuickSort(arr, 0, n-1);
    //HeapSort(arr, n);
    //CountingSort(arr, n);
    //BucketSort(arr, n, 3);
    RadixSort(arr, n);
    for (int i = 0; i < n; i++) {
      cout << arr[i] << " ";
    }
    cout << endl;
    return 0;
  }

  //测试用例
  // 2 3 1
  // 2 3 1 4
  // 2 2 1 4
  // 8 5 9 10 5 3 15 1 2  n == 9

展开

循环n-1次，每次从n - i个未排序数列中找到值最大的元素，放在已排序数列的左侧n - i - 1索引的位置
未排序数列在左，已排序数列在右
对于已排序的元素，最好复杂度为n

选择排序（Selection Sort）（比较排序）

  void SelectionSort(int arr[], int n) {
    for (int i = 0; i < n - 1; i++) {
      int curIndex = i;
      for (int j = i + 1; j < n; j++) {
        if (arr[j] < arr[curIndex]) {
          curIndex = j;
        }
      }
      swap(arr[i], arr[curIndex]);
    }
  }

展开

循环n-1次，每次从n-i个未排序数列中找到值最小的元素，放在已排序数列的右侧i索引位置
未排序数列在右，已排序数列在左
在查询过程中和BubbleSort不同的是，非通过swap查询最值元素

插入排序（Insertion Sort）（比较排序）

  void InsertionSort(int arr[], int n) {
    for (int i = 1; i < n; i++) {
      for (int j = i; j > 0; j--) {
        if (arr[j] > arr[j - 1]) {
          break;
        }
        swap(arr[j], arr[j - 1]);
      }
    }
  }

展开

每次将i索引元素插入到左边从i开始已排序数列中
未排序数列在右，已排序数列在左

归并排序（Merge Sort）（递归）

  void Merge(int arr[], int m, int l, int r) {//合并
    int* temp = new int[r - l + 1];
    int i = l, j = m + 1, index = 0;
    while (i <= m && j <= r) {
      if (arr[i] < arr[j]) {
        temp[index] = arr[i];
        i++;
      }
      else {
        temp[index] = arr[j];
        j++;
      }
      index++;
    }
    while (i <= m) {
      temp[index] = arr[i];
      i++;
      index++;
    }
    while(j <= r) {
      temp[index] = arr[j];
      j++;
      index++;
    }
    for (int i = 0; i < r-l+1; i++) {
      arr[l + i] = temp[i];
    }
    delete[] temp;
  }

  void MergeSort(int arr[], int l, int r) {
    //基本返回情况
    if (l >= r)return;

    //状态转移
    int m = (l + r) / 2;
    MergeSort(arr, l, m);//分解
    MergeSort(arr, m + 1, r);
    Merge(arr, m, l, r);
  }

展开

分解合并的思想
递归
- 函数功能：对数组lr区间排序
- 返回条件：数列只有一个元素，直接返回它
- 状态转移：从中间分解为2个有序数列，再合并为1个有序数列

快速排序（Quick Sort）（递归）

  void QuickSort(int arr[], int l, int r) {
    if (l >= r)return;
    int pivot = arr[l];
    int i = l, j = r;
    while (i < j) {
      while (i < j && arr[j] >= pivot)j--;
      while (i < j && arr[i] <= pivot)i++;//i指令要放在j指令后面
      if(i < j)swap(arr[i], arr[j]);
    }
    swap(arr[l], arr[i]);
    QuickSort(arr, l, i - 1);
    QuickSort(arr, i + 1, r);
  }

展开

每次从未排序数列中选择一个元素称为 “基准”，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面
递归：
- 返回条件：数列只有一个元素
- 状态转移：按照基准划分后，继续对左右数列分别快排
要注意ij交点的情况，
- 如果ij中间元素为0个，先让j–，i不变，i与l交换正确
- 如果ij中间元素为1个
  - 如果这个值属于j侧，j-2，i不变，i与l交换正确
  - 如果这个值属于i侧，j-1，i++，i与l交换正确
如果pivot每次都</>其他元素，那么为n^2的算法

三路快排（递归）

  void quickSort(vector<int>& nums, int left, int right){
      if(left > right)return;
      int pivot = nums[left];
      int l = left, cur = left, r = right;
      while(cur <= r){
          if(nums[cur] < pivot){
              swap(nums[cur], nums[l]);
              cur++;
              l++;
          }else if(nums[cur] > pivot){
              swap(nums[cur], nums[r]);
              r--;
          }
          else cur++;
      }
      quickSort(nums, left, l - 1);
      quickSort(nums, r + 1, right);
  }

展开

三路快排：
- 思想：
  - 4个指针pivot、l、cur指向left，r指向right
  - 循环条件cur<=r
  - l指针左侧维护<pivot的部分，r右侧维护>pivot的部分
  - 每次比较cur和pivot，根据</>swap cur和l/r，对l/r ++/–，如果<=，cur++
  - 对左右两部分数据递归，对于==的数据，不继续递归
- 适用于：适用于包含大量重复元素的数组，可以显著提高性能

堆排序（Heap Sort）（递归）

  void AdjustHeap(int arr[], int l, int r) {//调整堆
    if (l >= r)return;//少于一个节点不用调整
    int left = 2 * l + 1, right = 2 * l + 2, index = l;
    if (left <= r && arr[index] < arr[left])index = left;//超过r之外的已排序数列不调整
    if (right <= r && arr[index] < arr[right])index = right;
    if (index != l) {
      swap(arr[l], arr[index]);
      AdjustHeap(arr, index, r);//超过r之外的已排序数列不调整
    }
  }

  void BuildMaxHeap(int arr[], int n) {//构建堆
    for (int i = n / 2 - 1; i >= 0; i--) {
      AdjustHeap(arr, i, n - 1);
    }
  }

  void HeapSort(int arr[], int n) {
    BuildMaxHeap(arr, n);
    swap(arr[0], arr[n - 1]);
    for (int i = n - 2; i > 0; i--) {
      AdjustHeap(arr, 0, i);
      swap(arr[0], arr[i]);
    }
  }

展开

索引：
- 最后一个非叶节点（最后一个叶节点的父节点）：第n层节点的数量是<= n-1层节点数量 + 1，所以它的索引为节点总数n/2-1（x + x + 1 = n, 2x + 1 = n, x = n/2 - 1）
步骤：
- 映射（不用实际操作）：无序数列数组映射到完全二叉树，堆从左往右读取，树自顶向下，从左到右写入（一行行写）
- 构造大根堆：从以最后一个非叶节点为根的树开始，调整堆，直到以索引0为根的树调整完成为止（构造完成的并非单调递减的序列，虽然每个节点都>子孙，但兄弟可能不是正确排序，所以整体还是乱序的）
  - 调整堆（递归）：
    - 作用：在左右子树都为大根堆情况下，对根节点调整（根可能不遵守大根堆性质），使得整体重建为大根堆
    - 算法：若左右节点最大值 > 根节点值，则交换，并对子节点中被交换节点为根的树递归调用调整堆
- 交换：对于大根堆确定了未排序数列中的最大值元素，在根节点位置，通过它与第n - i个元素交换，从后往前放，作为已排序数列
- 排序：现在对于未排序数列中，左右子树仍是大根堆，但被交换后的根节点不在正确的位置，通过调整堆可以重建大根堆，获得新的最大值元素并交换，……循环直到排序完成

计数排序（Heap Sort）（存放分配）

  void CountingSort(vector<int>& arr, int n) {
    int mi = INT_MAX, ma = INT_MIN;
    for (int i = 0; i < n; i++) {
      if (arr[i] < mi)mi = arr[i];
      if (arr[i] > ma)ma = arr[i];
    }

    int count = ma - mi + 1;
    vector<int> c(count);
    for (int i = 0; i < n; i++) {
      c[arr[i] - mi]++;
    }
    for (int i = 1; i < count; i++) {
      c[i] += c[i - 1];
    }

    vector<int> d(n);
    for (int i = 0; i < n; i++) {
      d[--c[arr[i] - mi]] = arr[i];
    }
    for (int i = 0; i < n; i++) {
      arr[i] = d[i];
    }
  }

展开

找出待排序的数据中最大和最小的元素，确定额外开辟的C数组(计数器)空间的范围，
遍历数据对C计数数组计数C
对C数组所有的计数累加，确定区域右端位置
遍历元素分配给D数组
D数组复制给原数组

桶排序（Bucket Sort）（存放分配）

  void BucketSort(int arr[], int n, int k) {
    int mi = INT_MAX, ma = INT_MIN;
    for (int i = 0; i < n; i++) {
      if (arr[i] < mi)mi = arr[i];
      if (arr[i] > ma)ma = arr[i];
    }

    //存放
    k = (k <= 0 || k > n) ? n : k;
    int elementCount = ma - mi + 1;
    int maxElementForOneBucket = elementCount / k;
    k = (elementCount % k != 0) ? k + 1 : k;
    vector<vector<int>> buckets(k);
    for (int i = 0; i < n; i++) {
      int index = (arr[i] - mi) / maxElementForOneBucket;
      index = (index > k) ? k : index;
      buckets[index].push_back(arr[i]);
    }

    //排序
    for (int i = 0; i < k; i++) {
      CountingSort(buckets[i], buckets[i].size());
    }

    //分发
    int index = 0;
    for (int i = 0; i < k; i++) {
      for (int j = 0; j < buckets[i].size(); j++) {
        arr[index++] = buckets[i][j];
      }
    }
  }

展开

映射函数：将数据映射到桶中的函数，它决定算法的效率
确定数据范围
创建桶，
存放元素
分别对每个桶元素排序（使用其他排序算法）
数据拼接

基数排序（Radix Sort）（存放分配）

  #include <vector>
  #include <cmath>
  void RadixSort(int arr[], int n) {
    //最大值最小值
    int mi = INT_MAX, ma = INT_MIN;
    for (int i = 0; i < n; i++) {
      if (arr[i] < mi)mi = arr[i];
      if (arr[i] > ma)ma = arr[i];
    }
    
    //如果有负数，整体+abs（min复数）
    int offset = 0;
    if (mi < 0) {
      for (int i = 0; i < n; i++)arr[i] += (-mi);
      ma += (-mi);
      mi += (-mi);
      offset = (-mi);
    }

    //统计最大位数
    int maxBit = 0, temp = ma;
    while (temp != 0) {
      temp /= 10;
      maxBit++;
    }

    //存放+分配
    vector<vector<int>> vec(10);
    for (int i = 0; i < maxBit; i++) {
      //存放
      for (int j = 0; j < n; j++) {
        int index = arr[j] % (int)pow(10, i + 1) / (int)pow(10, i);
        vec[index].push_back(arr[j]);
      }
      //分配
      int index = 0;
      for (int j = 0; j < 10; j++) {
        for (int k = 0; k < vec[j].size(); k++) {
          arr[index++] = vec[j][k];
        }
        vec[j].clear();
      }
    }

    //如果有负数，整体-abs（min复数）
    if (offset != 0) {
      for (int i = 0; i < n; i++)arr[i] -= offset;
      ma -= offset;
      mi -= offset;
    }
  }

展开

按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位（右侧是低位）
每一次外循环，相当于把当前排序位按照从小到大的顺序排列存放

算法与数据结构

本文由作者按照 CC BY 4.0 进行授权

算法复杂度分析

排序算法

算法复杂度

冒泡排序（Bubble Sort）（比较排序）

选择排序（Selection Sort）（比较排序）

插入排序（Insertion Sort）（比较排序）

归并排序（Merge Sort）（递归）

快速排序（Quick Sort）（递归）

三路快排 （递归）

堆排序（Heap Sort）（递归）

计数排序（Heap Sort）（存放分配）

桶排序（Bucket Sort）（存放分配）

基数排序（Radix Sort）（存放分配）

热门标签

三路快排（递归）