101复习(6`物理仿真)

物理仿真

• 动画：渲染画面连续播放，>30fps
• 关键帧动画：中间帧通过插值技术生成
• 物理仿真：通过各种物理公式，计算网格体的位置/形变，通常和渲染分步实现
• 导数：
  • 数学表示:
    • f’(x)，dy/dx,
    • f’‘(x), d²y/dx²，d(dy / dx) / dx
  • 物理表示：
    • ẋ, dx/dt, 时间t为默认自变量
    • ẍ，d²x/dt²，d(dx / dt) / dt
    • x位置，ẋ 速度, ẍ 加速度
• 质点弹簧系统：
  • 一个弹簧左右连接两个质点ab，中间为弹簧，弹簧初始长度l
  • 胡克定律: F = k·x k劲度系数(取决于固体材料) ，x形变量
  • 弹簧受力分析
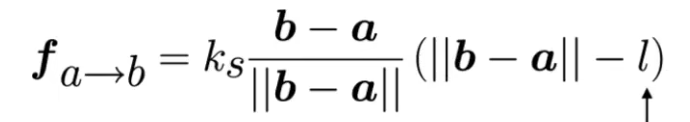
    • 把弹簧拉长，弹簧处于静止状态，因此ab受力平衡，a受到拉力 == a受到弹力，b受到拉力 == b受到弹力
    • 由于弹簧是一个整体，弹簧处于静止状态，因此a受到拉力 == b受到拉力，因此a受到拉力 == a受到弹力 == b受到拉力 == b受到弹力
    • 当ab拉力消失，ab不在受力平衡，将向内收缩，收缩过程中势能逐渐转为动能，速度越来越快，当到达原长，势能变为0，由于惯性ab继续运动，压缩弹簧，动能减少逐渐转变为势能，压缩到最大，动能为0，ab反向运动弹簧伸展，这样周而复始弹簧会不断伸缩
    • 为了让弹簧停止，需要添加摩擦力项，和ab的速度方向相反
    • 但如果将弹簧拉开，并让ab同时向右移动，这时ab摩擦力方向都左，这样并不能让ab恢复弹簧的原长度，仅能让ab不再向右移动
    • 所以摩擦力方向应该和相对运动方向相反，对于b来说，看相对a的变化，b受到的摩擦力：
      • kd表示摩擦力大小，负号表示和相对运动方向相反
      • 括号内点乘决定摩擦力大小的缩放
        • 如果相对a项右移动，归一化向量方向向右，速度为向右，同向点乘结果为1，
        • 如果相对a项左移动，归一化向量方向向右，速度为向左，反向点乘结果为-1
        • 假设b相对a做圆周运动，即b垂直于ab方向移动，虽然ab有速度，但相对弹力没有改变，因此不应该获得ab方向的摩擦力，公式中获得点乘结果为0，正是想要的结果
      • 最后的归一化向量，保证结果是向量
  • 模拟布料
    • 当用弹簧网格模拟布料，会出现两类错误的受力
      • 切片力：沿对角线拉伸弹簧会出现形变，而布料不会，可以在两个对角线方向增加较强（布料不会形变）弹簧，当被抻拉受到挤压时可以产生对抗力
      • 剪切力：跳格连接较弱（布料仍可以弯曲）弹簧，作为抵抗力
• 粒子系统
  • 创建粒子
  • 计算每个粒子受力
  • 更新每个粒子位置和速度
  • 清除粒子
• 单粒子模拟
  • 基础概念：
    • 速度场：横轴时间，纵轴位置，切线速度方向
    • 代数方程：含有未知数的等式，解是常数
    • 微分方程：含有未知函数及其 导数的等式，解是函数，常规微积分是“从函数求导数”，而微分方程是“从导数求函数”
    • 常微分方程：只有一个自变量的微分方程
    • 偏微分方程：含有两个或者多个自变量的微分方程
    • 几阶微分方程：最高阶导数是几阶导数
  • 问题：dx/dt = v（瞬时速度），已知起始位置x0，导数v，求自变量t对应的因变量x
    • 解一阶常微分方程：
      • 显示欧拉方法（用t1的位置和速度去估计t2位置和速度）
        • 把时间分为一个个小块，比如一个小块t1——t2，t2的位置 = t1的位置 + Δt * t1速度，t2位置的速度 = t1速度 + Δt * t1加速度
      • 中点法：（用t1的位置和t0.5的速度去估计t2位置和速度）
        • t0.5中点位置 = t1位置 + Δt/2 * t1速度，t2位置 = t1位置 + Δt * t0.5中点速度，t2位置的速度 = t1速度 + Δt * t1加速度
      • 自适应：（把一次欧拉分为两次欧拉，如果和一次欧拉方法结果差值 < 阈值，则不用继续分割）
        • t0.5中点位置 = t1位置 + Δt/2 * t1速度，t2位置 = t0.5位置 + Δt/2 * t0.5中点速度
      • 隐式欧拉（用t2的位置和速度去估计t2位置和速度）
        • t2位置 = t1位置 + Δt * t2速度，t2位置的速度 = t1速度 + Δt * t2加速度
        • 由于t2速度和t2加速度未知，因此需要解方程组
  • 稳定性：
    • 局部截断误差：每一步产生多少误差
    • 整体误差：局部误差累积
    • 欧拉方法是1阶方法，即局部截断误差为Δt^2，整体误差Δt, 随着Δt减小，误差会减小
    • 龙格库塔方法：（用来解常微分方程）
      • 
      • 4阶方法，因此误差很小
      • 公式里面的y可以换成上面x位置，n表示帧，h表示Δt，f(t,y)替换成f(t,x)速,k1k2k3k4系数
• 刚体模拟
  • 刚体：指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体
• 流体模拟
  • 流体：流体是指在微小剪切力的持续作用下能够连续变形的物质
  • 质点法：
    • 用很多刚体小球表示
    • 假设水不可被被压缩，那么任何一刻任何一个位置都可以知道密度，如果有密度和正常时刻密度不一样，就需要通过移动小球位置来修正密度