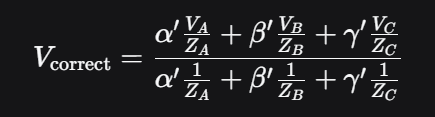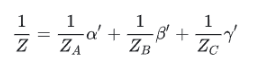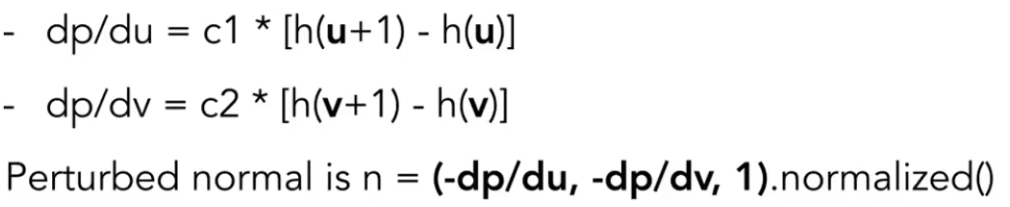101复习(4`渲染管线、纹理映射)

渲染管线

• GPU渲染流水线（for(阶段)）
  • 应用阶段CPU：（准备数据和状态）
    • 准备场景数据和状态
      • 顶点数据(顶点位置，法线方向，纹理坐标)
      • 摄像机（位置，方向，正交/透视，裁剪空间范围）
      • 光源（位置，数量，颜色，强度，方向，范围）
      • 资源（纹理，模型）
      • 渲染状态（测试规则，面剔除，背景色）
    • bind数据和状态
    • 调用drawcall，开始执行GPU渲染流程
  • 几何阶段GPU：（处理几何体）
    • 逐顶点vs（MVP，转换到裁剪空间）
    • 图元装配 (将顶点装配为基本图元：点、线、三角形等)
    • 逐顶点ts细分 (可选，将网格细分为多个网格)
    • 逐顶点gs几何（可选，对图元顶点增删改，性能开销大）
    • 裁剪：剔除视锥外的图元，生成新P点
    • 透视除法：将裁剪坐标转换为归一化设备坐标 (NDC)
    • 视口变换（转换到屏幕空间）
  • 光栅化阶段GPU：（颜色处理）
    • 栅格化（覆盖性测试，将图元转为片元，插值顶点属性）
    • 逐片元fs（计算颜色）
    • alpha测试
    • 模板测试
    • 深度测试
    • 颜色混合
    • 写入颜色缓冲区
• CPU渲染流水线（for(图元)）

纹理映射

• 纹理是一块数据，可以存储任何数据
• 纹理映射
  • 把一张纹理贴到模型表面（3维坐标映射到2维uv坐标，颜色值数据拷贝到对应位置）
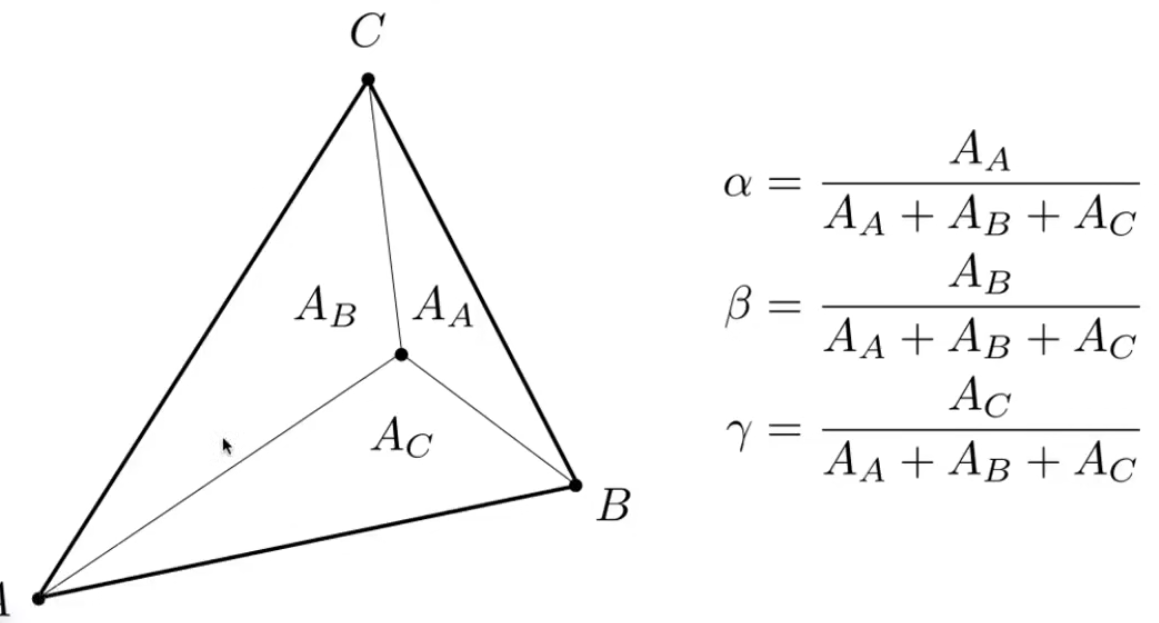
  • 如何计算内部像素映射的uv位置，根据三角形图元重心插值，三角形顶点对应的纹理坐标通常会预先定义好
• 重心插值
  • 插值时机：图元装配后，片元生成后，也就是光栅化阶段后
  • 3维
    • 视图空间重心坐标：对片元做数据插值，正确做法是在3维的视图空间的3D位置做插值，之所以是视图空间而不是在比如NDC空间中，是因为在投影变换后会导致不正确的插值结果，那么现在要对片元做空间转换，将它转换到视图空间，然后在3D空间计算重心坐标
    • 重心插值：aA + bB + yC,ABC为顶点属性，a+b+y == 1,a、b、y>0（如果不是非负，在三角形所在平面内）
  • 2维
    • 屏幕空间重心坐标：
      • 
      • 根据不相邻三角形面积/总面积
      • 三角形重心，为重心坐标(1/3,1/3,1/3)的位置，它将三角形面积分为3等分
      • 
      • 面积的计算可能不太容易，用这个公式计算重心坐标
    • 透视校正重心插值：
      • 
      • z_a, z_b, z_c是3个顶点在3维空间中顶点深度值，VaVbVc是顶点属性
      • 
      • 1/Z：近似了当前片元在视图空间的深度
• 屏幕分辨率 > 纹理分辨率，
  • 需要把纹理放大使得大小一致，放大时纹理的像素数量不变，像素大小变大，一个纹理像素对应多个屏幕像素，并通常查询到非整数坐标，
  • 邻近插值：四舍五入，多个屏幕像素查询同一纹理像素，形成的图像会产生一个个格子
  • 解决方法：
    • 双线性插值：
      • 对一个屏幕像素找到临近的四个纹理像素，2*2，可以根据这个uv点，首先四舍五入找到当前像素，看在当前像素的左上左下右上右下哪个方向找4个像素
      • 线性插值lerp：v0 + t(v1 - v0),t(0——1)， == tv0 + (1-t)v1
      • 水平2次线性插值，垂直一次线性插值
      • 这个x的值范围为0——1，因为两个像素中心距离最大为1
• 屏幕分辨率 < 纹理分辨率
  • 需要把纹理缩小使得大小一致，缩小时纹理的像素数量不变，像素大小变小，一个屏幕像素对应多个纹理像素，并通常查询到非整数坐标
  • 临近插值：四舍五入，一个屏幕像素大小（1*1，非点）覆盖更多的远处纹理像素，覆盖更少的近处纹理像素，形成摩尔纹，近处锯齿的走样
  • 解决方式：
    • 抗锯齿，但需要使用很多很多的采样点（比如512个）才能达到不错的效果，极度消耗性能
    • 范围采样：
      • 思想：可以找到屏幕像素覆盖的所有纹理像素的平均颜色值，作为屏幕像素颜色，但暴力法极度消耗性能，使用近似方法mipmap将减少性能消耗
      • 创建：从一张原纹理第0层新生成log2^n层纹理（n为原纹理max(width,height)的分辨率），每次生成的分辨率是上一次的1/4（width,height同时/2，如果width != height，短的到1为止不在变化，长的继续），像素大小为上一层的4倍，上一层每4个旧像素合成一个新像素，取像素平均值作为新像素的颜色值
      • 
      • 内存消耗：新增内存为原图的1/3，消耗非常小
      • 限制：只对正方形范围查询效果良好
      • 查询覆盖面积：
        • 方法一：找到uv像素和临近像素（上右），在uv纹理中映射的点，和计算连接向量模长，作为覆盖面积的长宽，这是因为两个像素采样点的距离为1，等于此像素的边长，根据它们估计此像素在uv中的覆盖面积是较为近似的
        • 方法二：将uv像素的4个顶点映射到uv中计算面积
        • 近似为正方形
      • 找到查询层
        • 根据像素面积，查询在哪一层会变为一个像素的大小，查询索引log2^n（n为覆盖面积的边长），在这层的uv位置获取颜色值（需要双线性插值），作为此像素颜色值
      • 非整数查询层
        • 三线性插值：如果查询到非整数层（覆盖面积边长非2的整数倍），分别在两整数层找到颜色结果，再根据覆盖面积接近两层像素大小的程度，做一次线性插值，形成均匀过渡
      • 问题：对于远处的物体，会完全模糊掉，因为它仅限正方形范围查询
        • 模糊原因：屏幕像素覆盖面积形状可能是长方形/不规则图形，方向正/斜
        • 
        • 各项异性过滤（不同方向上表现不同），和mipmap等比压缩不同，对长宽某一侧压缩，以便可以查询矩形区域, 但对于斜着的区域不友好，新的内存消耗是原本的3倍
• 漫反射贴图：物体基础颜色值
• 镜面光贴图：镜面反射的区域强度
• 法线贴图：详见其他章节
• 视差贴图：详见其他章节
• 凹凸贴图：
  • 通过修改法线从而使得模型表面的贴图产生凹凸的错觉
  • 如何根据高度图生成法线方向？
    • 从一维函数看，切线方向是求一阶导数，法线方向垂直于切线，即将切线方向旋转90°可得到法线方向（xy对换，将x加上负号），归一化
    • 
    • 对于2维来说，思想和一维一样，分别求两个方向的导数，再旋转90°得到法线方向，归一化
• 位移贴图：
  • 和凹凸贴图使用一致的纹理
  • 对顶点实际的移动
  • 需要顶点数量足够多，纹理分辨率足够大
  • 效果更好，性能消耗更多
• 深度贴图：存储深度值，常用于遮蔽关系，阴影生成……
• 环境贴图：
  • 记录所有方向的所有光源（无论直接光照/间接光照）
  • 假设所有光都来自很远处，这样不用考虑物体所在位置的影响
  • 通常用cubeMap/sphericalMap存储
  • 球体存储直接展开的扭曲问题：由于顶端周长小，中间周长大，展开到长方体上两侧会被拉伸，可以用正方体包裹球体，根据球心到球面点方向向量投射到立方体，展开立方体的6个面
• 3D纹理：空间任何一个点的纹理值，使得物体可以看到内部
• 噪声贴图：生成噪声算法纹理，使得物体表面变化具有随机感
• AO纹理：

函数

• 
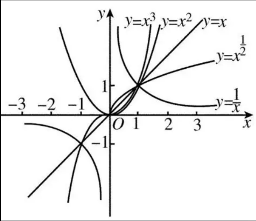
• 幂函数 x^a，x作为底数，a作为指数，一维函数
  • 正分数幂：x^(m/n) == sqrt(x^m)n
  • 负分数幂：x^-(m/n) == 1/sqrt(x^m)n
  • 小数次幂：小数转为分数
• 
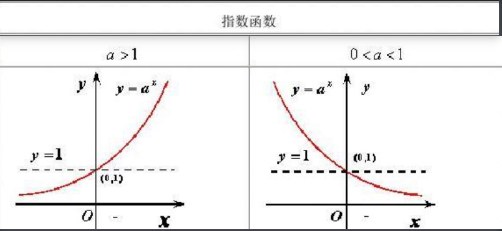
• 指数函数 a^x = y (a > 0 && a != 1)
  • 指数函数 a < 0时，负数的非整数指数幂在实数范围内没有定义，会导致函数断裂，破坏连续性，无研究意义
  • 指数函数 a == 0时，无论x取何值，结果为0，无研究意义
  • 指数函数 a == 1时，函数是线性的，无研究意义
• 
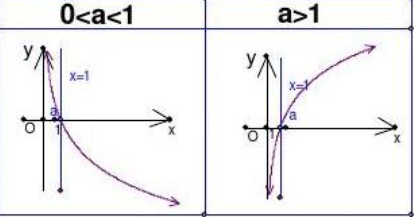
• 对数函数loga^y = x
  • lg:10为底的对数
  • ln：以无理数e（e=2.71828…）为底的对数，叫作自然对数
  • log2^n = x: n==1->0,n==2->1,n==4->2,n==8->3,n==16->4,n==32->5,n==64->6,n==128->7,n==256->8,n==512->9
    • x从0开始每次+1，n从1开始每次变为上一次的2倍
• 
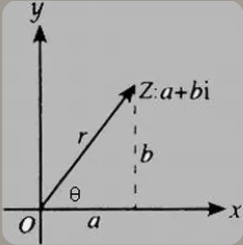
• 复数：
  • 虚数i^2 == -1
  • 复数表示法：形如a + bi为复数，实数与虚数的组合
  • 坐标表示法：实数是一维数，都在实数轴上，复数在二维空间，复数平面，x为实轴，y为虚轴，a画在x轴方向，b画在y轴方向