2`进制、位运算
进制
基础
- 最小到的传输单位bit位/比特
- 最小的存储单位是byte字节 == 8位
- 左边高位,右边低位
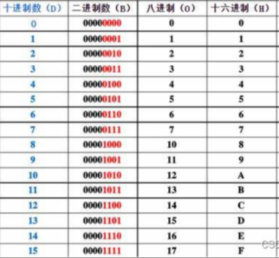
- 2,8,10,16表示范围:0——1,0——7,0——9,0——9 + A——F
- 前缀:0b/0B,0o/0O,无,0x/0X
- 后缀:b/B,o/O,d/D,h/H
- 0x00:0000 0000 ,0xff:1111 1111
- ACSII码(有128个字符,包括数字,字母,特殊符号),将字符与整数对应, 以便将这些字符转换为计算机可以理解的二进制码
数据范围
- 有符号数可以表示的范围是:-2^(bit-1) —— 2^(bit-1) - 1
- 比如8位:1111 1111 —— 0111 1111 :-2^7 —— 2^7 :-127 —— 127
- 1000 0000 == -0 ,0没有负数,我们用它表示-128 :-128 —— 127
- 无符号数可以表示的范围是:0 —— 2^(bit) - 1
- 比如8位:0000 0000 —— 1111 1111 :0 —— 2^8 : 0 —— 255
溢出处理:
- 整数超过所能表示的范围,会被高位截断(首先转换成二进制)
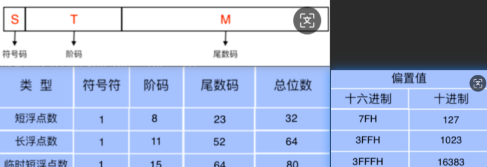
- 浮点数(包含整数和小数)
存储换算:
1 字节 (Byte) = 8 位 (bit)
1 KB (KiloByte) = 1024 Bytes 1 MB (MegaByte) = 1024 KB = 1,048,576 Bytes 1 GB (GigaByte) = 1024 MB = 1,073,741,824 Bytes(2^32 = 4GB, 2^64 = 1TB) 1 TB (TeraByte) = 1024 GB = 1,099,511,627,776 Bytes 1 PB (PetaByte) = 1024 TB 1 EB (ExaByte) = 1024 PB
内存基础
字长:CPU一次并行处理的二进制数据的最大位数,通常为32位和64位,体现计算效率 地址总线:物理线路,体现寻址能力,地址总线的个数,通常为32个和64个 寻址范围:最大可支持内存,2的N次方,n为地址总线的个数,2^32 = 4GB 按字编址:意味着以字节为单位对存储单元进行编号,也就是每个地址对应一个字节 存储容量 == 总内存
CPU,GPU区别
- CPU
- 25%的ALU(运算单元)、有25%的Control(控制单元)、50%的Cache(缓存单元)
- 特点:计算量小,计算复杂的运算较快,10个核左右
- 使用场景:少量的复杂计算(并不是说CPU不能处理图形,GPU不能处理计算,只是谁更适合哪个)
- GPU
- 90%的ALU(运算单元),5%的Control(控制单元)、5%的Cache(缓存单元)
- 特点:计算量大,计算复杂的运算非常慢,几千核(高度并行)
- 使用场景:大量的简单运算,不适合循环/分支
原码,反码,补码
用二进制表示数字和字符,如何正负性和运算呢?
1
2
正数1的原码为: 0 0000001
负数-1的原码为:1 0000001
展开
原码:二进制的首位当作符号位,[ 0 ]表示正数,[ 1 ]表示负数
1
2
3
4
5
6
7
就像10进制运算,超过9要进制一样,进制val/10, 保留val%10
val/2,val%2
2进制加法运算 :0+1=1,1+0=1,0+0=0,1+1 = 0(进制1,保留0)
12 + 2 = 14
1010
+ 0010
= 1100
展开
加法运算:
1
2
3
4
3 + (-5) = -2
0 0000011 原
+ 1 0000101 原
= 1 0001000 原 == -8
展开
减法运算:将减法转换为加法(例如3 - 5 = 3 + (-5)),但直接用原码计算的结果是错误的
1
2
3
4
5
6
7
8
-5的原码为:1 0000101
-5的反码为:1 1111010
3 + (-5) = -2
0 0000011 反
+ 1 1111010 反
= 1 1111101 反
1 0000010 原 == -2
展开
反码
- 为了保证结果正确,数学家规定所有参与运算的数均以反码形式存储和计算
- 正数反码与原码相同,负数的反码除符号位不变其余位取反
- 运算结果应再次转为原码
- 正数原码:与反码相同
- 负数原码:反码除符号位不变其余位取反
1
2
3
4
5
1 + (-1) = 0
0 0000001 反
+ 1 1111110 反
= 1 1111111 反
1 0000000 原 == -0
展开
- 但是它有时会出现问题,比如上面的用例,0没有负数
1
2
3
4
5
6
7
8
9
10
11
12
13
(-1)1 0000001 -> 1 1111110 -> 1 1111111
1 + (-1) = 0
0 0000001 补
+ 1 1111111 补
= 10 0000000 补 这里溢出了,最高位会被丢弃
0 0000000 原 == 0
(-1) + (-1) = -2
1 1111111 补
+ 1 1111111 补
=11 1111110 补 这里溢出了,最高位会被丢弃
1 1111110 -> 1 0000001 -> 1 0000010 原 == -2
展开
补码
- 补码正是用来解决+0和-0的问题,数学家规定所有参与运算的数均以补码形式存储和计算
- 正数补码与原码相同,负数的补码为反码再加上1
- 运算结果应再次转为原码
- 正数原码:与补码相同
- 负数原码:补码除符号位不变其余位取反,再加1
1
2
3
4
5
6
7
8
(-127) 1 1111111 -> 1 0000000 -> 1 0000001
-1 + (-127) = -128
1 1111111 补
+ 1 0000001 补
= 11 0000000 补 这里溢出了,最高位会被丢弃
1 0000000 -> 1 1111111 -> 10 0000000 原 这里溢出了,最高位会被丢弃
0 0000000 原 == 0//结果错误
展开
- 但是它有时会出现问题:
1
2
3
4
5
6
7
(-127->)
-1 + (-127) = -128
1 1111111 补
+ 1 0000001 补
= 11 0000000 补 这里溢出了,最高位会被丢弃
1 0000000 -> 0 1111111 -> 1 0000000 原 == -128
展开
- -128是特殊的,数学家想出了一种统一的新方式去求补码
- 对于 1000 0000 这个特殊值,全部取反(非反码)加1
进制转换
- 2,8,16 -> 10进制整数,小数
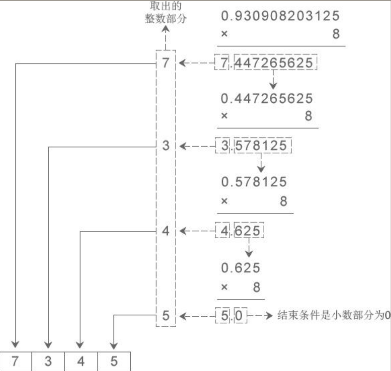
- 10 ->2,8,16进制整数,小数
- 2 -> 8,16进制
- 2 -> 8从后往前,每3位求和为一个位,不足应该在高位补0
- 2 -> 16从后往前,每4位求和为一个位
- 8,16 -> 2进制
- 8 -> 2每一个八进制位转换为3个二进制(10->2)
- 16 -> 2每一个十六进制位转换为4个二进制
- 8,16进制
- 通过10进制间接转换
位运算
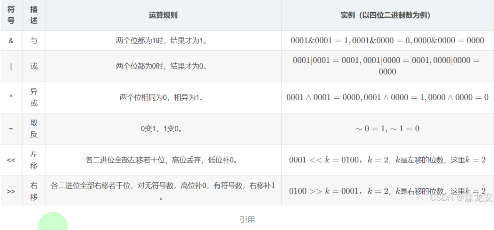
运算符
位操作
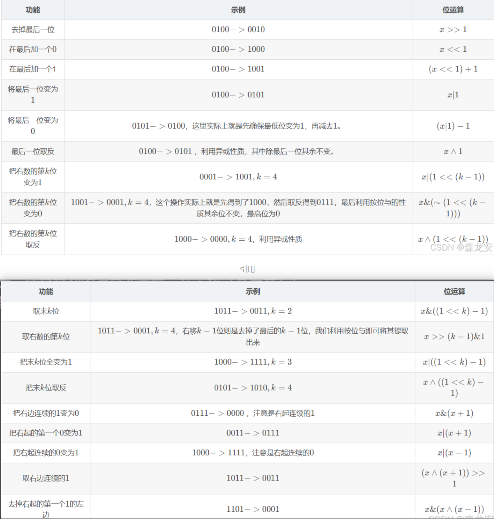
常见位运算
1
2
a << 1 ≡ a ∗ 2
a >> 1 ≡ a / 2
展开
乘除法
1
2
3
4
5
void swap(int &a,int &b){
a ^= b;
b ^= a;
a ^= b;
}
展开
交换
1
a & 1
展开
判断奇偶
1
~ a + 1
展开
对负数取绝对值
1
2
3
4
bool fun(int n) {
if (n <= 0) return false;
return (n & (n - 1)) == 0;
}
展开
判断是否是2^n
本文由作者按照 CC BY 4.0 进行授权