数据结构
数据结构
数据结构:用于存储和管理数据集合
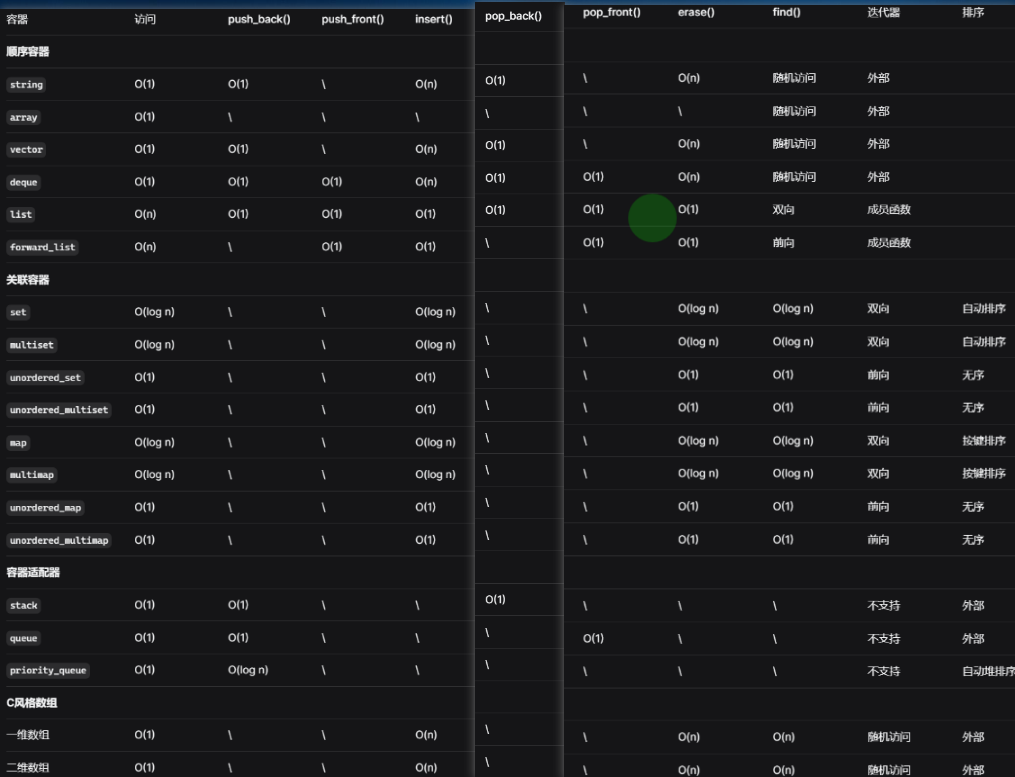
复杂度
操作:查询,插入,删除,首部添加删除,尾部添加删除
顺序容器
访问顺序不依赖元素值,而是依赖元素加入时间
字符串
C风格字符串(非容器)
1
2
3
4
5
6
7
char str1[] = "Hello";
char str2[10] = "World";
const char* str3 = "C-style";
strlen(str1);//6
strcpy(str2, "New");
if (strcmp(str1, "Hello") == 0) {}
strcat(str2, "!!");
展开
- 字符数组:const char[],const char*
- 以空字符’\0’结尾
- strlen()获取长度,不算空字符
- strcpy()赋值,传入的指针必须指向以空字符结尾的数组
- strcmp()比较,如果不用此函数,将比较指针
- strcat()拼接
- 更轻量
- 适用于与C API交换情况
string
1
2
3
4
5
6
7
8
9
std::string str2("World");
std::string str3(5, 'A');
std::string str1 = "Hello";
str1.size();//5
str1 = "New String";
str2 = str1;
if (str1 != str2){}
str1 += "This";
const char * str = s.c_str();
展开
- 可变长字符序列:类对象
- str.length()或str.size()获取长度,返回类型是size_type(无符号整数类型),通常用自动推断
- =赋值运算符 赋值
- 关系运算符 比较
- +/+= 拼接
- 转换到C风格字符串
- 范围for遍历序列元素
- []下标运算符 访问
- 更安全,更容易使用
数组
C风格数组(非容器)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//静态数组
int arr1[5];
int arr2[5] = {1, 2, 3, 4, 5};
int arr3[] = {1, 2, 3};
int static2DArr2[2][3] = {1,2,3,4,5,6};
int static2DArr2[2][3] = {
{1, 2, 3},
{4, 5, 6}
};
int size = sizeof(arr2) / sizeof(arr2[0]);
for (int i = 0; i < 5; ++i) {
heapArr[i] = i * 10;
}
std::vector<int> vec2(std::begin(c_array), std::end(c_array));
//动态数组
//一维数组
// 初始化
int* arr = new int[n];
//释放
delete[] arr;
//二维数组
// 初始化
int** arr = new int*[row];
for(int i=0;i<row;i++)
{
arr[i] = new int[col];
}
//释放
for(int i=0;i<row;i++)
{
delete[] arr[i];
}
delete[] arr;
展开
- 固定连续内存,编译期确定大小
- 多维数组:数组的元素是数组
- 静态动态数组,动态数组可以动态调整大小,p[i] == *(p + i) != *p + i
- sizeof()获取大小
- memset批量初始化
- 需逐个元素/memcpy,赋值
1
2
3
4
5
6
7
//一维传参:
void func(type arr[]) / void func(type arr[n]) / void func(type *arr)
//二维传参:
void func(type arr[][y]) / void func(type arr[x][y]) / void func(type (*arr)[y])
//数组赋值给指针
type a[];
type* arr = a;
展开
- 作为参数/赋值时,退化为指针(指向数组的首元素地址),丢失大小信息,无法通过 sizeof(arr) 获取数组真实大小
- 解决方式:
- 额外传递长度参数
- type (&arr)[n],type (&arr)[Rows][Cols]通过引用传递数组
- 解决方式:
- 转换到向量
array
1
2
3
4
std::array<int, 5> arr = {5, 2, 8, 1, 9};
arr.size();
arr.front();
arr.back();
展开
- 兼容STL,初始化指定元素类型和容器大小
- 固定连续内存,编译期确定大小
- size()获取大小
- =赋值运算符 赋值
- []下标运算符,访问首个,末尾元素
- 比C风格数组更安全
- 没有灵活的内存管理
vector
1
2
3
4
5
6
7
8
9
10
std::vector<int> vec1;
std::vector<int> vec3(5, 10);
std::vector<int> vec2 = {1, 2, 3, 4, 5};
vec2.size();
vec.push_back(4);
vec.pop_back();
vec.insert(vec.begin() + 1, 99);
vec.erase(vec.begin() + 2);
vec.resize(8, 100);
int* arr = vec.data();
展开
- 向量/可变大小数组:类模板,动态大小
- size()获取大小
- =赋值运算符 赋值
- 添加,弹出,插入,删除,调整大小……
- 后进先出,先进后出
- 转换到C风格数组
- 更安全,更容易使用
- string和vector由于元素在连续的内存空间,特定位置查询很快,但向特定位置(除了尾部)增/删会非常耗时(在增/删后需要移动其后的所有元素,以保证连续存储,可能还要分配额外的空间)
链表
forward_list
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
std::forward_list<int> fl1;
std::forward_list<int> fl3(5, 10);
std::forward_list<int> fl4(fl2);
std::forward_list<int> fl2 = {1, 2, 3, 4, 5};
for (auto it = fl2.begin(); it != fl2.end(); ++it){}
for (int val : fl2){}
fl.front();
auto it = fl.begin();
std::advance(it, 2);
*it;
fl.push_front(0);
fl.insert_after(it, 99);
fl.insert_after(it, {100, 200, 300});
fl.erase_after(it);
auto first = fl.begin();
auto last = fl.begin();
fl.erase_after(first, last);
fl2.remove(2);
fl.sort();
fl.reverse();
fl3.merge(fl4);
展开
- 单向链表
- 没有size获取大小的操作,只能遍历获取
- 通过for范围/迭代器来遍历
- 访问第一个元素,移动迭代器访问特定元素
- 向开头插入,向指定位置插入
- 删除后面的元素,删除范围内元素,删除所有特定值的元素
- 排序,反转,合并两个有序链表
list
1
2
3
4
5
6
7
8
lst.push_back(1);
lst.pop_back();
lst.back();
for (auto it = lst2.rbegin(); it != lst2.rend(); ++it){}
auto it = lst.end();
--it;
lst1.splice(lst1.end(), lst2);
lst.resize(5);
展开
- 双向链表
- 后面添加/删除/访问
- 反向遍历
- 反向移动
- 拼接到末尾
- 调整大小
- 链表在任何位置增/删会很快,但不支持随机访问(如果要访问指定元素,只能遍历链表),链表的内存开销比string和vector都要大,考虑到内存开销,如果不需要反向操作用forward_list
队列
deque顺序容器
1
2
3
4
5
6
7
8
std::deque<int> dq;
dq.push_back(30);
dq.front();
dq.back();
dq[1];
dq.pop_front();
dq.pop_back();
dq.insert(dq.begin() + 1, 25);
展开
- 双端队列
- 特定位置查询很快,但向特定位置(除了首部尾部)增/删会非常耗时
关联容器
通过元素值来存储和访问
集合
存储单个值,通常作为去重,无映射关系
1
2
3
4
5
std::set<int> s = {3, 1, 4, 1, 5, 9};
std::multiset<int> ms = {3, 1, 4, 1, 5, 9};
std::unordered_set<int> us = {3, 1, 4, 1, 5, 9};
std::unordered_multiset<int> ums = {3, 1, 4, 1, 5, 9};
auto it1 = s.find(3);
展开
set
- 有序,自动按键升序排序
- 底层实现:红黑树
- 查找时间:O(log n)
- 可以有序遍历
- lower_bound,upper_bound范围查询
multiset
- 允许重复
- 删除所有匹配元素
- 内存占用较多
unordered_set
[ˈɔrdərd]
- 无序,不会自动排序
- 查找时间:O(1)
- 用于快速查询
- 内存消耗较多
unordered_multiset
哈希
存储pair<const Key, Value>键值对,映射关系
1
2
3
4
std::map<std::string, int> m = {
{"apple", 5}, {"banana", 3}, {"apple", 10}
};
m["apple"] = 5;
展开
map
multimap
- 不支持[]操作符
unordered_map
unordered_multimap
容器适配器
由已有容器类型封装,使其看起来像另一种类型
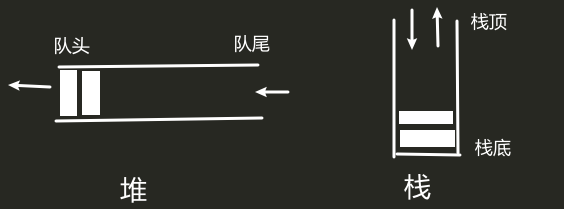
堆/队列:队头做删除操作,在队尾做插入操作,LIFO:先进先出,后进后出
栈:仅能在栈顶进行插入和删除操作,把另一端称为栈底,FIFO:先进后出,后进先出
栈
1
2
3
4
5
std::stack<int> stk;
std::stack<int, std::vector<int>> stk2;
std::stack<int, std::list<int>> stk3;
stk.push(1);
stk.top();
展开
stack
- 底层容器:vector/list/deque
- 接口相对vector比较少,语义更明确,有LIFO访问限制,防止意外访问
堆/队列
queue
1
2
3
4
5
std::queue<int> q;
std::queue<int, std::list<int>> q2;
q.push(1);
q.front();
q.back();
展开
- 接口相对vector比较少,语义更明确,有FIFO访问限制,防止意外访问
priority_queue
1
2
3
4
std::priority_queue<int> pq;
pq.push(30);
pq.top();
pq.size();
展开
- 优先队列
- priority_queue< type, container, function>元素类型,底层容器(缺省),比较方式(缺省)
- 元素根据其优先级大小有序排列,优先级高的元素会优先出队,而不是像普通队列那样遵循FIFO原则
- 优先队列也称为堆heap,分为大顶堆和小顶堆(默认底层容器是数组,默认是最大堆),堆的本质是完全二叉树
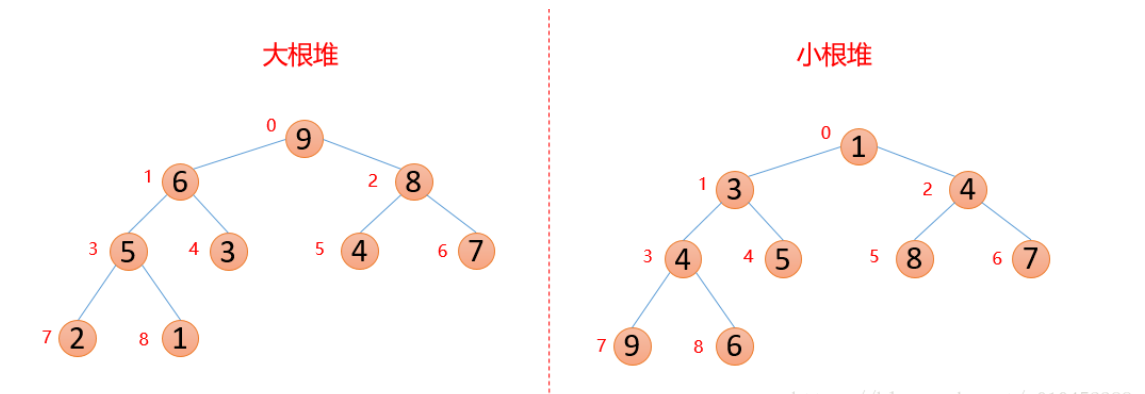
大顶堆和小顶堆
- 大顶堆:arr(i)>arr(2 * i+1) && arr(i)>arr(2*i+2),每个结点的值都大于其左孩子和右孩子结点的值
- 小顶堆:arr(i)< arr(2 * i+1) && arr(i)< arr(2*i+2),每个结点的值都小于其左孩子和右孩子结点的值
- 比较函数:
- c++提供了两个内置比较函数:less(<号)->构造大根堆->降序(默认),greater(>号)->构造小根堆->升序
工具
pair
1
2
3
4
5
std::pair<int, std::string> p1(1, "Alice");
std::pair p2(2, "Bob");
auto [id, name] = p1;
p1.first = 100;
p1.second = "David";
展开
- 对
- 键值对,固定2个元素,map元素类型是pair
- 通过first, second访问
- 可以作为函数多返回值
tuple
1
2
3
4
5
6
std::tuple<int, std::string, double> t1(1, "Alice", 95.5);
std::tuple t2(2, "Bob", 88.0);
std::get<1>(t1);
std::tuple<int, int> x(1, 2);
std::tuple<int, int> y(1, 3);
(x < y);
展开
- 元组
- 编译器确定数量
- get<N>()访问
- 可以作为函数多返回值
tie
1
2
3
4
5
6
7
8
9
10
11
12
13
//tie解包
auto student = std::make_tuple(1, "Alice", 95.5);
int id;
std::string name;
double score;
std::tie(id, name, score) = student;
//最简洁
auto student = std::make_tuple(1, "Alice", 95.5);
auto [id, name, score] = student; //会创建变量
//手动方式
id = std::get<0>(student);
name = std::get<1>(student);
score = std::get<2>(student);
展开
- 绑定
- 创建tuple/pair的引用,将它们的值解包到变量中
自定义
树
- 基本概念
- 祖先:从根到结点的唯一路径上的任意结点
- 子孙;如果a是b的祖先,则b是a的子孙
- 双亲:最接近的祖先
- 孩子;最接近的子孙
- 兄弟:有共同双亲的节点
- 深度:从根结点开始自顶向下逐层累加的()
- 高度:从叶结点开始自底向上逐层累加的
- 度:一个结点的孩子个数
- 性质:
- 节点n,边数n-1
- 第h层节点数量 = <h的所有层节点数量 + 1
- 对于树节点编号,是从上到下,从左到右
- 深度高度和层级都从索引0开始:
- 第k层最多有2^k
- 高度为h最多有2^(h + 1) - 1个节点
- 深度高度和层级都从索引1开始:
- 第k层最多有2^(k - 1)
- 高度为h最多有2^h - 1个节点
- 二叉树:
- 每个结点至多只有两棵子树
- 分类:
- 斜树:所有的结点都只有左子树的二叉树
- 满二叉树:所有层的结点个数都是最大值,有2^h - 1个节点,
- 完全二叉树:除最后一层外,其他层的结点个数全部达到最大值,且最后一层的结点从左侧填充
- 父节点索引从0开始:
- 父节点索引i:左孩子:2 * i + 1, 右孩子:2 * i + 2
- 左/右节点i:父节点:(i-1)/2
- 结点i所在层次为log2^i
- 具有n个(n>0)结点的完全二叉树的高度为log2^n
- 父节点索引从1开始:
- 父节点索引i:左孩子:2 * i为偶数, 右孩子:2 * i + 1为奇数
- 左/右节点i:父节点:i/2
- 结点i所在层次为log2^i + 1
- 具有n个(n>0)结点的完全二叉树的高度为log2^n + 1
- 父节点索引从0开始:
- 二叉搜索树:左子树上所有结点的关键字均小于根结点的关键字;右子树上的所有结点的关键字均大于根结点的关键字
- 平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过1
- 遍历方式:
- 先序:根左右
- 中序:左根右
- 后序:左右根
- 层级:
图
- 基本概念:
- G图,V节点集合,v节点,E边集合,uv边
- 分类:
- 有向图:若E是有向边的有限集合
- 无向图:若E是无向边的有限集合
- 简单图:不存在重复边,不存在顶点到自身的边
- 多重图:两个结点之间的边数多于一条
- 完全图:有n ( n − 1 ) / 2 n(n -1)/2n(n−1)/2条边的无向图称为完全图,任意两个顶点之间都存在边
- 连通图:
- 若从顶点v到顶点w有路径存在,则称v和w是连通的
- 若图G GG中任意两个顶点都是连通的,则称图G GG为连通图
- 遍历方式:
- 深度搜索DFS:
- 广度搜索BFS:
空间数据结构
详见其他章节
迭代器
1
for(auto it = s.being(); it != s.end(); it++){}
展开
- 迭代器不是指针,但类似于指针
- 主要用于容器元素访问
- []下标运算符只能有限容器访问,迭代器适用于所有STL容器(List,set),支持STL算法
- 操作:
- begin()获取容器首个元素的迭代器
- end()获取容器尾元素后的下一个位置的迭代器(不存在的元素)
- *iter,解引用返回iter指向的元素引用
- ->,获取iter指向元素的成员
- ==,!=,比较两个iter是否指向同一元素
- ++,–,移动到容器元素的下一位,上一位
- +,-,+=,-= 一个整数值,仍得到迭代器
- iter - iter,返回迭代器之间的距离
- iter >, >=,<,<= iter,所指位置前后关系
- 迭代器类型:iterator非常量指针,const_iterator常量指针,begin/end是否返回const由对象是否是const决定
本文由作者按照 CC BY 4.0 进行授权