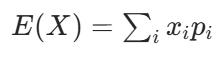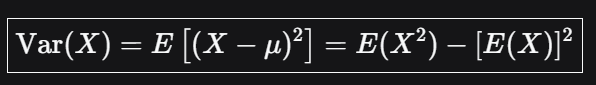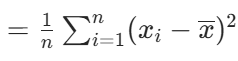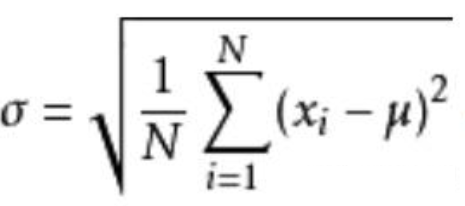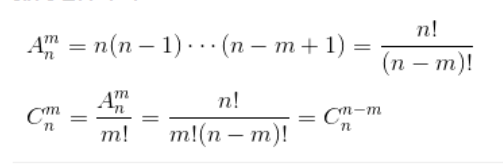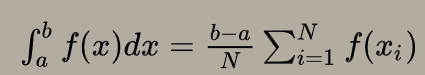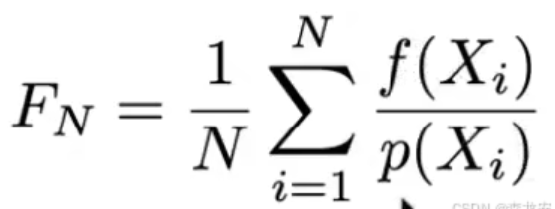数学(1`概率与统计学)
概率与统计学
样本、事件
- 样本空间Ω:一次实验所有试验可能结果的集合(去重结果,比如掷骰子有6种可能结果)
- 样本点:样本空间的元素(某个结果)
- 事件A:样本点子集(符合某种条件的结果集合)
- 互斥事件:两个事件是不相交的关系A∩B=∅,一个样本结果不会同时属于两个事件
- 掷骰子,把123点作为事件A,把456点作为事件B,任何结果都不会使得两个事件同时发生
- A和B发生的概率P(AB)=P(A)+P(B),越加越多,通常用或,如果要证明是否是互斥事件,则比较两侧结果是否相等
- 相交事件:两个事件是相交的关系,两个事件可以同时发生,
- 掷骰子,把1234点作为事件A,把456点作为事件B,结果4会使得两个事件同时发生
- 对立事件: 两个事件互斥,并且并集构成所有可能结果
- 掷骰子,把123点作为事件A,把456点作为事件B,任何结果要么事件A发生要么事件B发生
- 对立事件一定是互斥事件,但互斥事件不一定是对立事件
- 独立事件:结果互不影响的事件
- 掷2次骰子,第一次掷的结果不会影响下一次掷的结果
- AB同时发生的概率P(A+B)=P(A)×P(B),越乘越少,通常用且
- 互斥和独立之间没有直接关系
- 依赖事件:两个事件相互影响
- 互斥事件:两个事件是不相交的关系A∩B=∅,一个样本结果不会同时属于两个事件
随机变量
- 将样本空间中的每一个样本点映射到实数的函数,以确保每个样本点都能被唯一实数对应
- 用大写字母表示X/Y……,它的取值映射了样本空间所有可能结果,用xi表示
- 离散型:结果取值有限个,可数
- 连续型:结果取值无限个,不可数
- X = x, x表示某个结果映射的实数值
- P(X = x),某结果x的概率
均值、中位数、众数
- 总体均值μ:使用所有试验结果计算平均值(不去重)
- 样本均值x-bar:抽取样本结果估计平均值(不去重)
- 中位数:数据排列后中间位置的结果,当数列为偶数取两个中间值的平均值(不去重)
- 众数:数据中出现频率最高的结果,当不唯一时,多个数字都是众数(不去重)
期望
- 期望:E(X)是每个 结果xi * 对应概率pi 的总和
- 区别:
- 均值:实际试验结果的平均值
- 期望:是根据概率估计的平均值
- 复合函数期望:
- E(f(X)) = ∫ f(x)p(x) dx, X随机变量,p(x)概率密度函数,f(X)关于X的函数
- 方差和期望关系:
方差
方差Var(X): 衡量一组数据离散程度,数据波动越大,方差就越大
μ总体均值,xi是第i次结果,平方保证差异非负,看绝对值的差异,求和再/n平均差异
标准差:因为刚才把每个差值都平方化,我们取方差的平方根,用来直观的和原始数据比较
加法乘法概率法则
- 加法法则:用于计算互斥事件的概率,比如车牌号一个位置有字母26+数字10的选择,字母和数字是互斥事件,选择任何一个结果不可能即是字母又是数字
- 乘法法则:用于计算独立事件的概率,比如28种口味冰激凌和4种顶料,冰激凌和顶料是相交事件,一种圣代属于AB两个集合,AB是独立事件,选择哪个冰激凌并不影响选择哪个顶料,28*4=112种组合
排列组合
- 排列:对于n个元素,选择k个元素的方式,不同的顺序为不同排列(和顺序有关),比如123和321是不同排列
- 组合:对于n个元素,选择k个元素的方式,不同的顺序为相同组合(和顺序无关),比如123和321是相同组合
公式:m -> k
- 阶乘:
- 0! = 1
- n! = (n - 1)! × n
概率分布
- 事件概率:符合事件的样本点个数/所有样本点个数
- 概率分布:描述了随机变量所有可能取值对应的概率
- PMF:概率质量函数,用来描述离散型随机变量在各个取值的概率
- PDF:概率密度函数,用来描述连续型随机变量的dΔ(a——b区间面积)的概率
- CDF:累积分布函数,是PDF的积分,用来描述任何随机变量在<=xi值的概率
- 频率分布条形图:用在离散型随机变量,横轴为xi取值,纵轴为概率
- 频率分布直方图:用在连续型随机变量离散化后的区间,横轴为xi(a——b)区间,纵轴为概率
- 二项分布
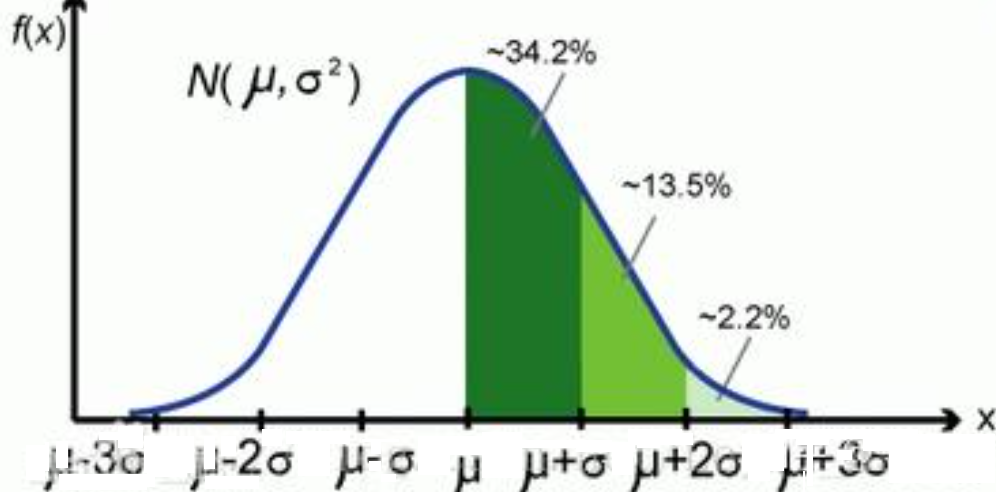
- 正态分布
解积分
有时积分难以解析求得积分结果,我们可以通过估计来计算
大数定律:指选择一个无偏(完全随机)的样本子集估计整体,会得到一个相对接近真相的答案,以下两种解积分方法正是建立在大数定律的基础上
黎曼积分
黎曼积分的思想是将定积分ab区间围成的面积,分割为N个小长方形求面积和
每个小长方形的x坐标用(x1,x2……xn)表示,其中(a-b)/N 作为小长方形宽,f(xi)作为高
其中因为每个小长方形宽均等,因此可以将(a-b)/N 提到求和外,结果是一致的
另一种理解的思想就是把1/N提取出来,也就是计算每个大长方形(b-a)的宽度 * fxi的高度,最后*1/N求均值
蒙特卡洛积分
蒙特卡洛积分思想依旧用长方形估计面积,但是进行了加权(概率函数自定义),因此小长方形的宽不再均等
1·为什么乘以1/N?
每个大长方形加权求和后需要平均, 就如同黎曼积分的第2种理解方式,通过 * 1/N 求均值
2·为什么除以pdf而非乘pdf?
先看简单的均等pdf情况,每个概率为1 / (b-a),那么fx /(1 / (b-a),即fx * (b-a),也就是每次都以(b-a)作为长方形的宽,最后将求得的每个大长方形求平均面积,这和黎曼的思想是一样的
也就是虽然用除法,但可以依旧理解为 * 宽度,只不过作为分母来说,概率越大,分母越大,值越小 * 更小的宽度(例如pdf == 5/10 == 1/2 == 0.5 宽度为2倍) ,* 更大的宽度(例如pdf == 2/10 == 1/5 == 0.2 宽度为5倍)
采样
对于无偏采样(完全随机)随着样本数量的不断增加,我们最终将收敛到积分的精确解
对于有偏采样(伪随机)会以更快的速度收敛,但是由于其有偏性,可能永远不会收敛到精确解
收敛速度:在相同的样本下,具有更准确的结果 / 得到相同的结果,用更少的样本
重要性采样
重要性采样正属于有偏采样的一种,可以使得在对积分结果贡献大的区域进行更多的采样,从而提高积分估计的准确性和效率
低差异序列
低差异序列 / 拟随机序列,该序列生成的仍然是随机样本,但样本分布更均匀,能够更有效地覆盖积分区域,使用低差异序列生成蒙特卡洛样本时,称为拟蒙特卡洛积分,具有更快的收敛速度
常见类型:
- Van der Corput 序列:通过反转自然数序列的base−n表示来构造的
- Halton 序列:基于不同底数(通常为质数)的 Van der Corput 序列生成
- Hammersley :是基于 Van Der Corput 序列,该序列是把十进制数字的二进制表示镜像翻转到小数点右边而得
- Sobol 序列:每一个维度都是由底数为2的 radical inversion 组成,但每一个维度的 radical inversion 都有各自不同的矩阵