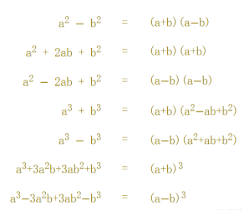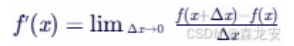数学(微积分)
微积分
微分是把整体分拆为小部分,导数可以求解函数的 极值点,凹凸性,拐点等
积分是把小部分组合到整体,积分可以求解函数的 面积,体积,曲线长度,最大小值等
lim极限
函数Q(x) = y:对于一个函数Q(x),当x取某些值时不能得到返回值
可以近似表示结果:(x->a) lim f(x) = L,当x趋近于a时,函数Q(x)极限是L
求极限的方式:
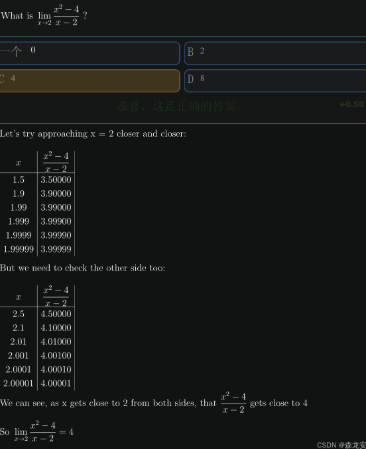
一、代入法
直接带入x / 带入x的临近值不断逼近答案
二、因式分解
可以将Q(x)转化为因式形式,从而带入求极限
因数:两个正整数相乘,那么这两个数都叫做积的因数,或称为约数。
因式分解:将表达式Q(x)转化为因式形式:
恒等式
比如:Q(x) = 4x^2 - 9 = (2x)^2 - (3)^2
->根据(a+b)(a-b) = a^2 - b^2 = (2x+3)(2x-3)
直到不能再分解为止
三、共轭
共轭:是把两个项之间的正负号倒转:3x + 1 -》 3x - 1
如果Q(x)是分式形式,上下都乘以 分子/分母 的共轭
四、无穷大
当x->∞时,求极限的方法:
- 非分数形式(看多项式Q(x)的最高指数项)
- 如果指数>=0,极限/ -∞(最高指数项的正负号)
- 如果指数<=0,极限 0
- 分数形式
- 如果分子 < 分母指数,极限为0
- 如果分子 > 分母指数,极限 / -(最高指数项的正负号)
- 如果分子 == 分母指数,极限为最高指数的项的系数相除
导数
一次导数 / 微分:
(Δy,Δx,dy,dx->0)
极限表示:当Δx趋近于0时,函数(y的增量 / x的增量)的极限
导数表示:f’(x)= dy/dx ,f(x) 的导数等于 dy / dx,’ 也可以记为d / dx
几何意义:
函数某一点的局部变化率
表示函数值随自变量x变化的快慢程度,是切线的斜率:dy/dx,而非两点斜率:(y2 - y1) / (x2 - x1)
求导:
f(x)的表达式已知,可以将x替换为x + Δx,获得新的表达式
将两个表达式带入极限公式,当Δx趋近于0是,表达式的值
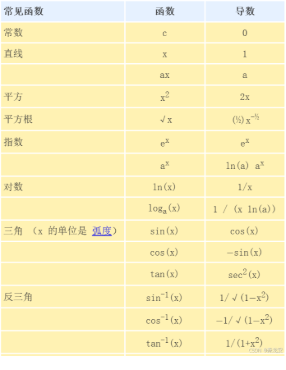
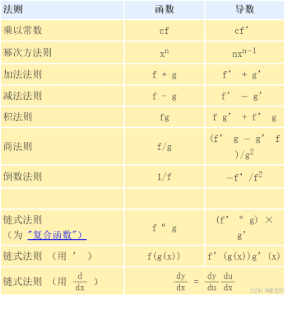
常见函数的导数:
导数法则:
二次导数 / 二次微分:
二次导数:是函数的导数的导数
f’‘(x) d(dy / dx) / dx
求导:
先求函数的导数,再求导数的导数
可微分,不可微分
可微分:存在导数-》转换为lim形式有极限-》左边极限 == 右边极限
几何意义上是否可微分:切线方向是确定的,且函数是连续的
极大值,极小值
一阶导数:==0时,为极点
二阶导数:小于 0 是极大值,大于 0 是极小值,==0检测失败
例子:
函数f(x) = 5x^3 + 2x^2 − 3x,求极大值和极小值
一次导数f’(x)(根据导数法则):15x^2 + 4x − 3
当导数==0即,15x^2 + 4x − 3,==0时,x = −3/5 或= +1/3,
二次导数 f’‘(x) (再次求导) : 30x + 4
在 x = −3/5:小于 0,为极大值,在 x = +1/3:大于 0,为极小值
上凹下凹,拐点
从直观上看:
下凸:开口向上的曲线,称为上凹,或称为下凸,形状为 ∪;
上凸:开口向下的曲线,称为下凹,或称为上凸,形状为 ∩;
从切线角度:
下凸:过任一1点的切线都在曲线弧之下
上凸:过任一1点的切线都在曲线弧之上
从割线角度:
下凸:在区间(a,b)对应内的曲线弧上任意两点的割线线段都在该两点间的曲线弧之上
上凸:在区间(a,b)对应内的曲线弧上任意两点的割线线段都在该两点间的曲线弧之下
用线性插值表示割线: ta + (1−t)b,(t 的值是从 0 到 1的集合,即线段的所有点)
从导数角度:
一次导数:
若导数连续增大,函数是 下凸
若导数连续减小,函数是 上凸
二次导数:
下凸:二次导数大于0
上凸:二次导数小于0
拐点:在下凸(上凸)变成上凸(下凸)的一个点
积分
基本定义:
定积分主要研究如何由 积分区间(被积函数)来求取一个数值,它可以代表面积或体积
不定积分主要研究如何由已知的函数(被积函数)来求取另一个函数 ,常用于计算曲线长度,最大小值等
相反关系 已知一个函数2x,求积分,已知x^2 的导数是2x,所以2x积分为x^2
∫ 2x dx = x^2
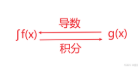
∫ f(x) dx = g(x) + C
∫ :积分符号,f(x):被积函数,dx积分的方向是 x-.>0,g(x):积分结果函数,C是积分常数(因为有很多函数的导数都相同)
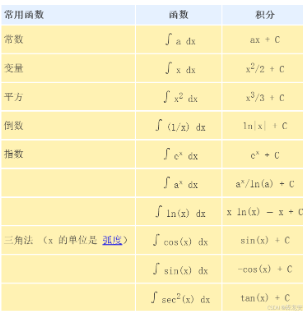
常见函数的积分
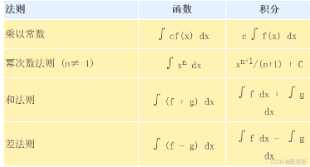
积分法则
分部积分法
∫u v dx = u∫v dx −∫u’ (∫v dx) dx
换元积分法
∫ f(g(x)) g’(x) dx -> ∫ f(u) du
求面积
如何求定积分/给定区间函数面积?
给定函数,先求出不定积分,然后将ab分别带入不定积分中,求b的结果 - a的结果